Transformaciones geométricas
Dgpad-colombia incluye 5 transformaciones geométricas: traslación, rotación, simetría axial, simetría central y homotecia.
La simetría axial se encuentra en el menú contextual de recta, la simetría central en el menú contextual de punto, la traslación en el menú contextual de vector, la rotación y la homotecia en el menú contextual de Expresión.
Estas transformaciones se aplican a puntos, segmentos, rectas, semirrectas, vectores, círculos, arcos y polígonos
Traslación

La traslación se construye con respecto a un vector, por eso la herramienta está en el menú contextual de los vectores. Es decir, para poder utilizar la herramienta es necesario haber creado un vector (menú contextual de Punto).
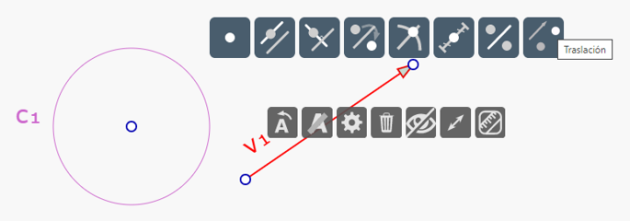
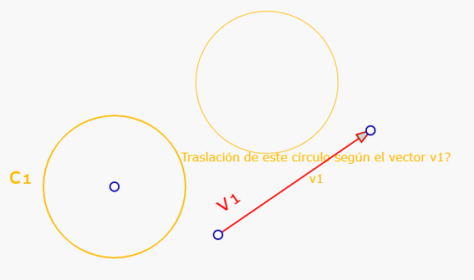
Por ejemplo, tenemos en la pantalla el vector v1 y un círculo c1. Si queremos construir la traslación de c1 según el vector v1, es necesario tocar el vector para hacer aparecer el menú contextual:
Se toca (SIN SOLTAR) la herramienta traslación.
Aparece un punto negro, traslación del punto que estamos señalando en la pantalla según v1, y el mensaje 'Traslación de un nuevo punto según el vector v1?'
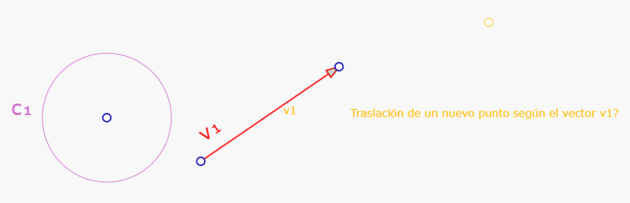
SIN SOLTAR, se lleva el cursor (el dedo) hasta el círculo c1.
El mensaje cambia a 'Traslación de este círculo según el vector v1?' y aparece el círculo traslación de c1.
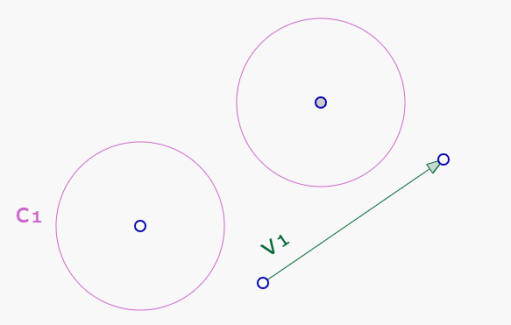
Teniendo iluminado el círculo c1, se suelta y queda construido la traslación de c1 según v1
Rotación

La rotación se construye con respecto a una expresión con un número que determina la medida del ángulo de rotación.Es decir, para poder utilizar la herramienta es necesario haber creado una expresión con un número y luego tocarla para mostrar el menú.
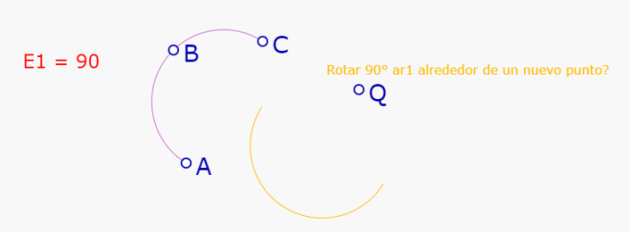
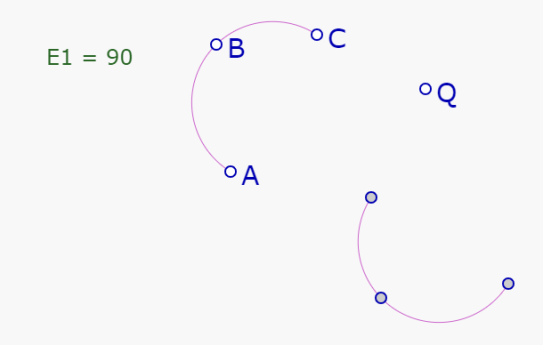
Por ejemplo, tenemos en la pantalla la expresión E1=90 (ángulo de la rotación), un arco ABC (que será rotado) y un punto Q (centro de rotación). Si queremos construir la rotación de 90 grados de P alrededor de Q, es necesario tocar la expresión E1 para hacer aparecer el menú contextual:
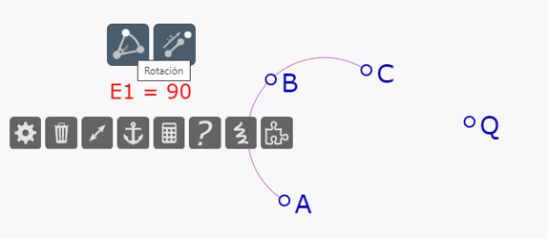
Se toca (SIN SOLTAR) la herramienta rotación.
Aparece el mensaje 'Rotar 90° un nuevo punto'
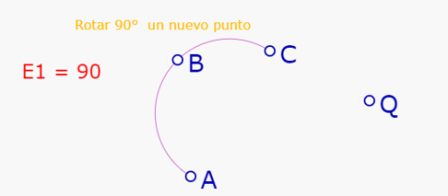
SIN SOLTAR, se lleva el cursor (el dedo) hasta el arco ABC.
El mensaje cambia a 'Rotar 90° este arco'
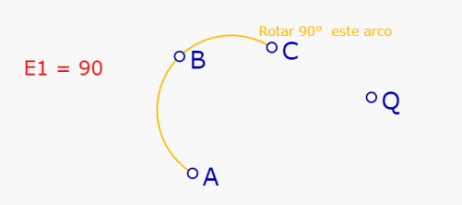
Al soltar, aparece nuevamente el icono de Rotación y el letrero cambia a 'Rotación de 90 grados de este arcp alrededor de un nuevo punto'
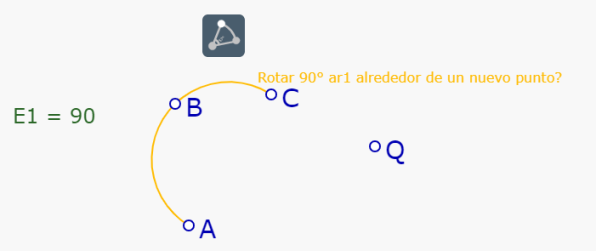
Se toca (SIN SOLTAR) la herramienta.
Aparece un arco que es la rotación de ABC alrededor del punto que estamos señalando en la pantalla y el mensaje 'rotar 90° ar1 alrededor de un nuevo punto?'
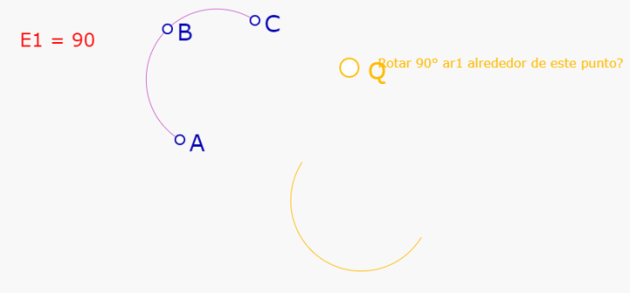
SIN SOLTAR, se lleva el cursor (el dedo) hasta el punto Q.
El mensaje cambia a 'Rotar 90° ar1 alrededor de este punto?'
Teniendo iluminado el punto Q, se suelta y queda construido el arco rotación de ABC de 90° alrededor de Q.
NOTA:
En las rotaciones los ángulos son 'orientados'; es decir, el sentido de la rotación depende del signo de la medida del ángulo. Las rotaciones de ángulo positivo se hacen en sentido antihorario y las de signo negativo en sentido horario.
Homotecia

Una homotecia es una transformación no isométrica; es decir, que no conserva las medidas. Precisamente, la homotecia lo que hace es agrandar o achicar los objetos.
La homotecia se construye con respecto a una expresión con un número que determina la razón de la homotecia. Es decir, para poder utilizar la herramienta es necesario haber creado una expresión con un número y luego tocarla para mostrar el menú.
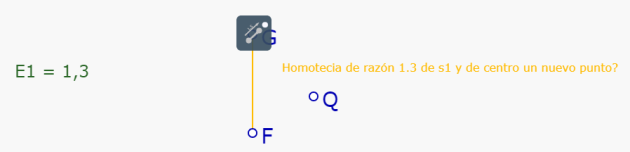
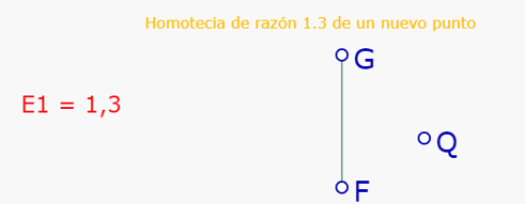
Por ejemplo, tenemos en la pantalla la expresión E1=1,3 (razón de la homotecia), un segmento FG (al que se aplica la homotecia) y un punto Q (centro de homotecia). Si queremos construir la homotecia de razón 1,3 de FG con respecto a Q, es necesario tocar la expresión E1 para hacer aparecer el menú contextual:

Hay que tocar el icono de Homotecia, SIN SOLTAR. Aparece el letrero 'Homotecia de razón 1,3 de un nuevo punto?
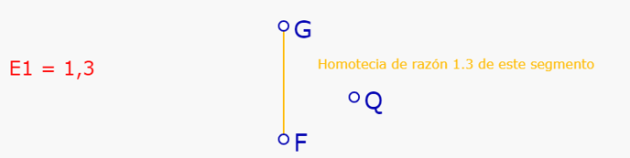
SIN SOLTAR, moverse hasta seleccionar FG.
El mensaje cambia a 'Homotecia de razón 1.3 de este segmento'
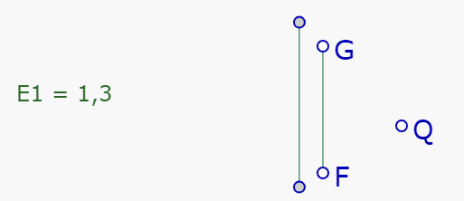
Al soltar, aparece nuevamente la herramienta homotecia y el mensaje cambia a 'Homotecia de razón 1.3 de este s1 y de centro un nuevo punto?'
Se toca (SIN SOLTAR) la herramienta y se lleva el cursor hasta el punto Q.
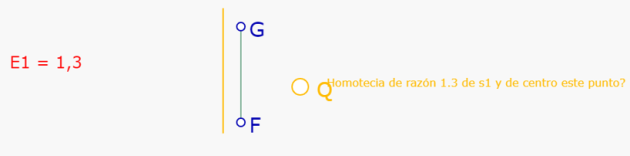
El mensaje cambia a 'Homotecia de razón 1.3 de s1 y de centro este punto?' y aparece el segmento homotético de FG.
Teniendo iluminado el punto Q, se suelta y queda construido el segmento homotético de FG con respecto a Q, de razón 1.3
NOTA:
Las homotecias pueden ser positivas o negativas. Si la razón de homotecia es negativa, el punto centro de homotecia quedará entre el punto al que se aplica la homotecia y el punto homotético.
Simetría axial y simetría central
Estas dos transformaciones están explicadas en Herramientas de Construcción de Recta y Herramientas de Construcción de Punto respectivamente