1.3.2 Tarea de experimentación con cantidades enteras. Construcción de la representación gráfica.
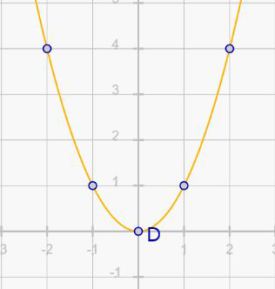
Primero se presenta una tarea de experimentación con números enteros; se presenta dos parábolas y se pide al estudiante que modifique el valor del parámetro \(a\) a partir de una lista desplegable que mostrará solo valores enteros, de tal manera que una parábola quede superpuesta a la otra.
Las parábolas fueron construidas de la misma manera que en el la actividad anterior (ver sección 1.1.2) utilizando la herramienta "cónica por 5 puntos", y las expresiones unidad, a y Random, construidas previamente. Para éste, a y Random corresponden a los valores de la amplitud de las parábolas a modificar y referente, respectivamente. Las parábolas compartirán el mismo vértice que estará fijo en el origen, teniendo en cuenta que lo que se modificará será la amplitud. Los 5 puntos necesarios para la construcción de la parábola a modificar son:
[x(O),y(O)], con A como el vértice de la parábola.
[x(A)+Unidad,y(A)+a*Unidad],
[x(A)+2*Unidad,y(A)+4*a*Unidad]
[x(A)-Unidad,y(A)+a*Unidad],
[x(A)-2*Unidad,y(A)+4*a*Unidad]
En esta tarea se deja visible el punto [x(A)+Unidad,y(A)+a*Unidad] y [x(A)+Unidad,y(A)+Random*Unidad], siendo estos los referentes para que el estudiante logre establecer la amplitud de las parábolas.
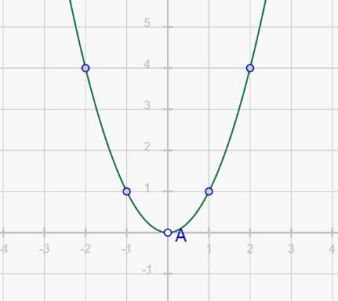
La parábola referente se construye análogamente a la parábola a modificar, con la variación de que los puntos diferentes al vértice no se modifican con a, sino con Random.
[x(O),y(O)], con A como el vértice de la parábola.
[x(A)+Unidad,y(A)+random*Unidad]
[x(A)+2*Unidad,y(A)+4*random*Unidad]
[x(A)-Unidad,y(A)+random*Unidad],
[x(A)-2*Unidad,y(A)+4*random*Unidad]