Segundo ejemplo
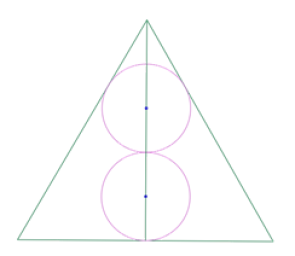
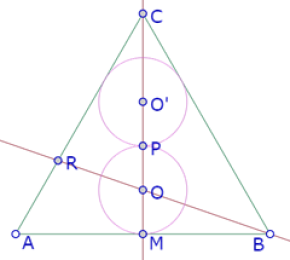
Se trata de reproducir esta imagen, donde pueden identificarse un triángulo equilátero con una de sus alturas, dos círculos congruentes que tienen sus centros sobre esa altura; uno de los círculos es tangente a dos lados del triángulo y al otro círculo, el otro círculo es tangente al tercer lado del triángulo y al primer círculo.
Primera solución
Parte I: experimentación para encontrar una construcción exacta
Comenzamos haciendo una construcción aproximada, a partir del triángulo equilátero y su altura.
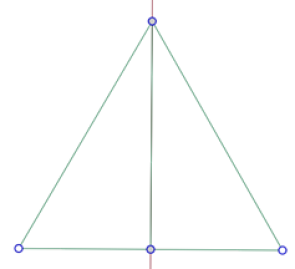
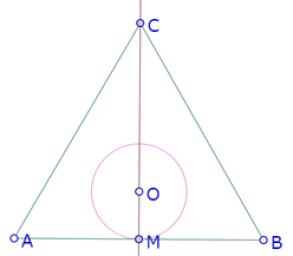
Construimos un punto O sobre la altura MC, que será el centro del segundo círculo. Como ese círculo debe ser tangente a AB, debe pasar por M.
Como el otro círculo debe ser tangente a este y del mismo radio, construimos la segunda intersección de este círculo con la altura (P) y el simétrico (central) de O con respecto a ese punto (O’); luego el círculo de centro O’ que pasa por P.
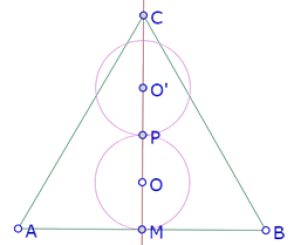
Acomodamos el punto O para lograr perceptivamente la tangencia del círculo de centro O’ con los lados AC y BC del triángulo.
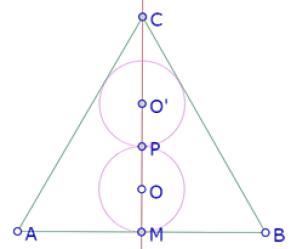
Para obtener una construcción exacta, es necesario determinar la posición de O que garantice que el círculo de centro O’ sea tangente a AC y BC.
Procedemos entonces a buscar perceptivamente otras propiedades que se cumplen cuando el círculo de centro O’ parece ser tangente a AC y BC.
Construyendo la segunda intersección de ese círculo con la altura del triángulo, parece que la altura queda dividida en 5 segmentos iguales.
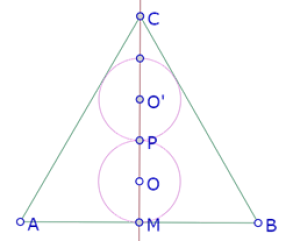
El punto O entonces debe quedar en la posición en la que OM=MC/5.
Para verificar experimentalmente esa conjetura, vamos a hacer una construcción a partir de esa propiedad.
Utilizando el teorema de tales podemos construir esa posición.
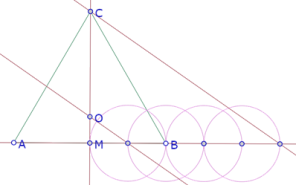
Y luego verificamos si los dos círculos resultantes cumplen con las condiciones del problema.
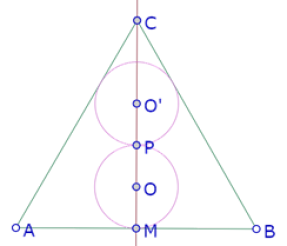
Aunque perceptivamente el círculo de centro O’ que pasa por P parece ser tangente a AC y BC, es necesario verificar esa tangencia más allá de la percepción.
Podemos por ejemplo, construir la intersección entre el círculo y los dos segmentos
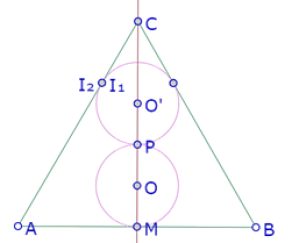
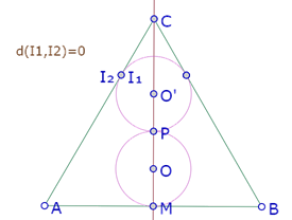
¿Eso significa que el círculo no es tangente al segmento AC? No necesariamente, pues los dos puntos pueden estar exactamente en la misma posición. Procedemos entonces a medir la distancia entre esos dos puntos.
Otra verificación diferente que podemos hacer es construir la recta perpendicular a AC que pasa por O’ y el punto de intersección de esa recta con el segmento AC. Si la distancia de ese punto a O’ es el radio del círculo, eso confirma que ese punto es un punto del círculo, y por lo tanto el círculo es tangente a AC.
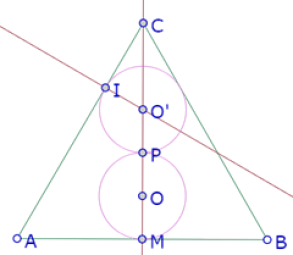
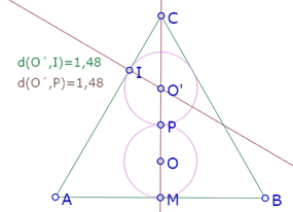
Una tercera manera de verificar la tangencia es construir la recta perpendicular a AC por O’ y el punto de intersección I entre esa recta y el círculo. Finalmente, medir el ángulo O’IC. Si ese ángulo es recto, entonces el círculo de centro O’ es tangente a AC.
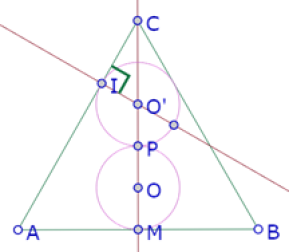
Hemos entonces confirmado experimentalmente que el círculo de centro O’ que pasa por P es tangente a AC. Y como O’ está sobre la bisectriz del ángulo ACB, entonces es equidistante de AC y BC, por lo cual el círculo también es tangente a BC.
Pero aquí no termina el trabajo en la solución del problema, pues esta construcción se hizo con base en hipótesis de propiedades que deben cumplirse, propiedades que encontramos de manera perceptiva en una construcción aproximada. El rigor matemático nos exige renunciar a toda hipótesis basada únicamente en la percepción. Así que necesitamos dar un fundamento deductivo a las hipótesis que formulamos a partir de la percepción.
Parte II: experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
Ahora tenemos que buscar una justificación deductiva de la hipótesis experimental que sirvió de base para nuestra construcción exacta: OM=MC/5.
Sabemos que los dos círculos son congruentes y tangentes entre sí, de manera que MO=OP=PO’=O’P’. Tenemos que demostrar que P’C=O’P’.
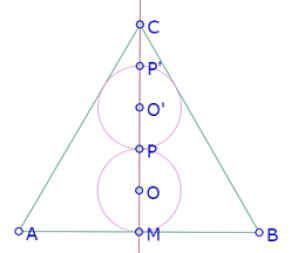
Ahora bien, si el círculo de centro O’ que pasa por P es tangente a la recta AC, necesariamente la recta AC es perpendicular a O’I (donde I es el punto de tangencia).
Así que el triángulo O’IC es rectángulo.
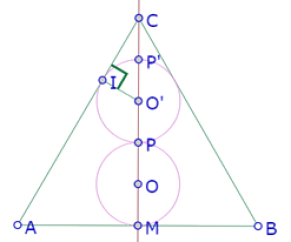
Por otra parte, la recta CM, altura del triángulo ABC, también es bisectriz del ángulo ACB, porque el triángulo es equilátero. De manera que el ángulo O’CI mide 30° y el ángulo CO’I mide 60°. Es decir, el triángulo O’IC es la mitad de un triángulo equilátero. Por lo tanto, la hipotenusa es el doble del cateto menor: CO’=IO’*2. En otras palabras, el segmento CO’ es el doble del radio del círculo y por lo tanto O’P’=P’C, por lo que MC=5OM, o MC/5=OM.
Segunda solución
Parte I: experimentación para encontrar una construcción exacta
Examinemos ahora una segunda solución del mismo problema.
Volvamos a nuestra construcción aproximada inicial:
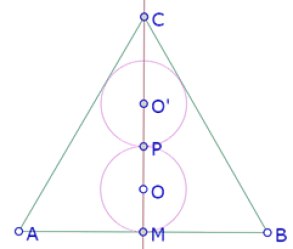
Otra posibilidad de búsqueda de propiedades es intentar relacionar la posición de los puntos O, P, O’ con los lados del triángulo ABC.
Por ejemplo, si trazamos la recta BO, corta el segmento AC en un punto R.
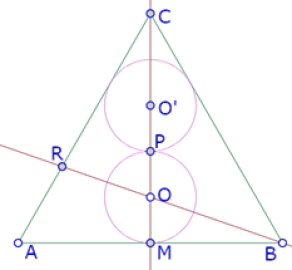
Podemos verificar si el segmento AR cabe un número entero de veces en el segmento AC. Si construimos el círculo de centro R que pasa por A, R’ la segunda intersección de ese círculo con AC, y el círculo de centro R’ que pasa por R, vemos que ese círculo parece pasar por el punto C.
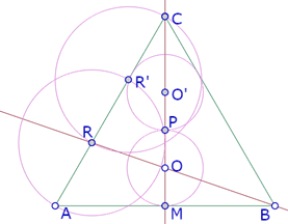
Entonces el segmento AR sería la tercera parte del segmento AC. Para verificar, vamos a realizar la construcción a partir de esa propiedad.
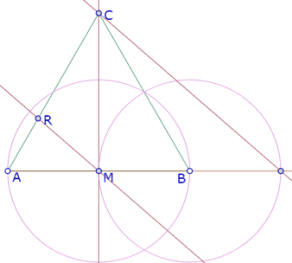
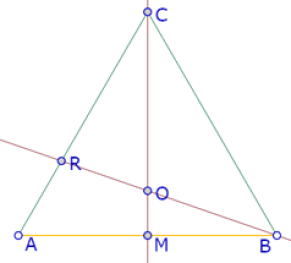
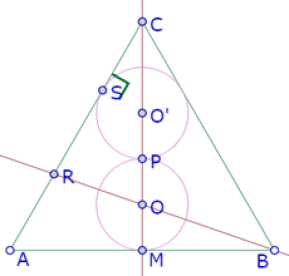
Para verificar la tangencia del círculo de centro O’ con el lado AC, construimos la intersección de esos dos elementos (S) y el ángulo O’SC.
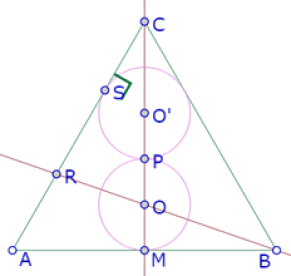
Al arrastrar A o B, se sigue manteniendo la tangencia.
Parte II: experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
Ahora tenemos que buscar una justificación deductiva de la hipótesis experimental que sirvió de base para nuestra construcción exacta: AR=AC/3.
Para demostrar la conjetura según la cual la recta BR, con 3AR=AC, corta la mediatriz de AB en el punto O que garantiza que el círculo de centro O’ será tangente a AC y BC, bastará con demostrar que el punto O construido de esa manera divide el segmento MO en una razón 1:4 (que implica que 5OM=MC).
Podemos aplicar el teorema de Menelao, según el cual si una recta corta los tres lados de un triángulo ABC en los puntos F, D y E respectivamente, entonces
Consideremos el triángulo AMC, y la recta RB que corta AB en B, MC en O y AC en R.
Entonces según el teorema de Menelao
Pero por construcción
Así que
Que es lo que queríamos demostrar