Sexto ejemplo
Dados un triángulo equilátero y un segmento cualquiera, construir un hexágono equilátero que tenga tres de sus lados no consecutivos sobre los lados del triángulo y todos sus lados sean congruentes con el segmento dado.
Parte I: experimentación para encontrar una construcción exacta
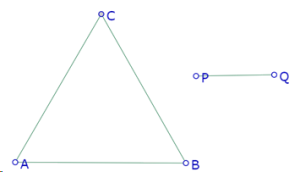
Hacemos una construcción de lo dado en el enunciado del problema:
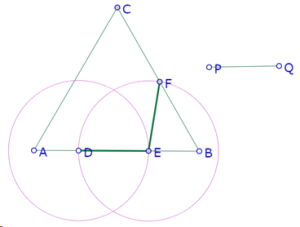
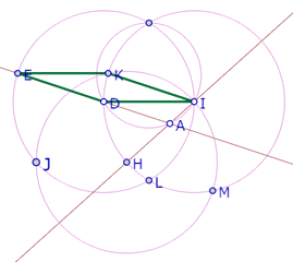
Y comenzamos la construcción del hexágono equilátero pedido: si el hexágono es DEFGHI, pondremos DE sobre AB, FG sobre BC y HI sobre CA.
Construimos el punto D como punto sobre el segmento AB, y usamos la herramienta compás para construir el punto E tal que DE=PQ.

Luego usamos la herramienta círculo (centro/punto) para construir el punto F sobre BC, tal que EF=DE.
De la misma manera construimos los segmentos FG, GH, HI
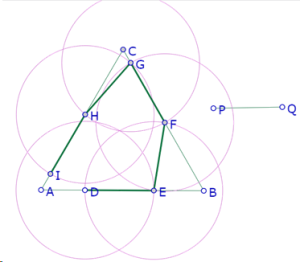
Como puede observarse a simple vista, el segmento ID no tiene la longitud de PQ.
Para conseguir que perceptivamente ID=PQ, construimos el círculo de centro I que pasa por H y movemos D hasta hacer que quede sobre ese círculo.

Esta figura no es una construcción exacta, puesto que al arrastrar el punto D, se pierde la propiedad ID=PQ, necesaria para que DEFGHI sea equilátero[1].
Podemos explorar un poco qué sucede al modificar la longitud del segmento PQ.
[1] Es posible que se produzca un malentendido con respecto a la interpretación del término ‘hexágono equilátero’. En efecto, es muy poco común el uso del adjetivo ‘equilátero’ para calificar polígonos diferentes al triángulo (triángulo equilátero), lo que podría hacer pensar que el término ‘hexágono equilátero’ es equivalente a ‘hexágono regular’. Pero en realidad para que un polígono sea regular, debe ser ‘equilátero’ (sus lados deben ser iguales) y ‘equiángulo’ (sus ángulos deben ser iguales). El triángulo es el único polígono en el que no es posible tener solo una de las dos condiciones. Aunque no sea de uso corriente, un rectángulo es un cuadrilátero equiángulo, y un rombo es un cuadrilátero equilátero.

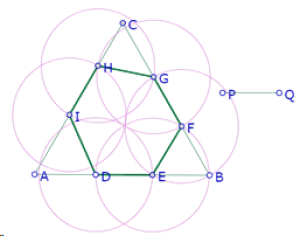
Al achicar el segmento PQ, vemos que hay un momento en el que no es posible obtener la propiedad DI=PQ para ninguna posición del punto D.
La longitud mínima de PQ parece ser AB/3, caso en el que el hexágono sería regular.
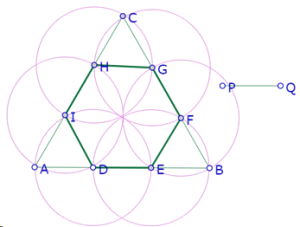
Ahora, si agrandamos el segmento PQ
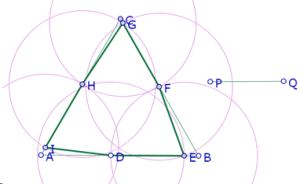
puede verse que cuando la longitud de PQ se acerca a AB/2, el hexágono tiende a convertirse en el triángulo ABC.
¿Qué sucede cuando PQ>AB/2?

Ya no habrá intersección entre el lado BC y el círculo de centro F que pasa por E.
Pero esta situación corresponde a una interpretación estricta de ‘lado del triángulo’ como un segmento. También es posible interpretar ‘lado del triángulo’ como una recta, en cuyo caso sí habría intersección.
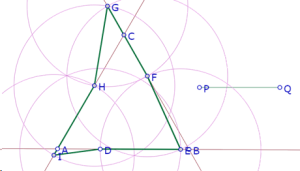
Y en este caso es posible acomodar el punto D para obtener perceptivamente la condición DI=PQ
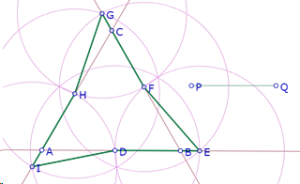

No parece existir un límite superior para la longitud de PQ.
Hasta ahora, gracias a la experimentación con una figura no exacta, podemos afirmar que para cada longitud del segmento PQ existe un hexágono equilátero como el pedido en el problema, con la salvedad de que PQ no puede ser menor a AB/3, y en los casos en los que PQ>AB/2 hay que considerar los lados del triángulo ABC como rectas, no como segmentos. Pero aún no hemos resuelto el problema, ya que no sabemos garantizar que el hexágono DEFGHI sea equilátero; solo logramos garantizar la congruencia de 5 de sus lados. En otras palabras, nos falta encontrar la posición exacta del punto D sobre AB, que garantiza que DI=PQ.
Para encontrar esa posición exacta del punto D, podemos continuar experimentando con la figura aproximada, con distintas longitudes del segmento PQ, en la posición de D que hace que perceptivamente el hexágono sea equilátero, y buscar otras propiedades que parecen cumplirse en esa posición. Hasta encontrar alguna(s) propiedad(es) que permitan construir el punto D de manera exacta.
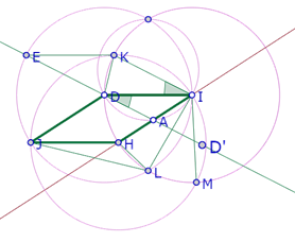
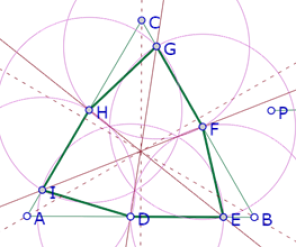
Retomemos la figura aproximada del comienzo:
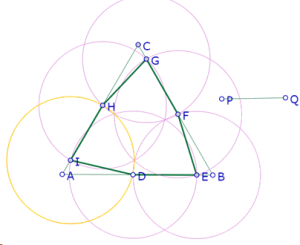
Podemos observar en esa imagen que los triángulos ADI, EBF y GCH parecen ser congruentes. También que los seis círculos construidos para garantizar la igualdad de los lados del hexágono parecen cortarse de a cuatro en los vértices de un triángulo equilátero.
Podemos verificar si estas dos propiedades parecen cumplirse para otras longitudes de PQ.

Con PQ más pequeño, parecen cumplirse esas dos propiedades.
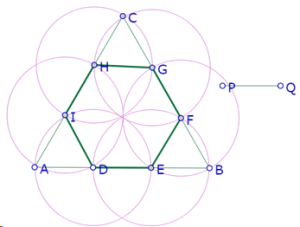
Cuando PQ se acerca a AB/3, todos los círculos parecieran cortarse en un solo punto, y los triángulos ADI, EBF, GCH parecen ser equiláteros.
Ahora examinemos nuestras conjeturas para casos en los que PQ>AB/2
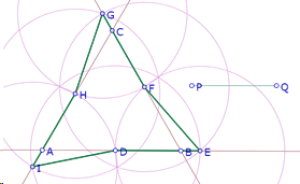

En estos casos, las dos propiedades parecen cumplirse, sólo que los triángulos ADI, BEF y CGH están en el exterior de ABC, y el triángulo equilátero formado por las intersecciones de los círculos también tiene sus vértices en el exterior de ABC.
Además, observamos que el triángulo DFH también parece ser equilátero. Y si revisamos las imágenes anteriores podemos ver que el triángulo IEG también parece ser equilátero.
Sin embargo, no sabemos cómo relacionar esas dos propiedades con la posición del punto D[1]. Así que continuamos la búsqueda de propiedades que se cumplen en el caso en el que el hexágono es equilátero. Como a simple vista no hemos encontrado otras propiedades, vamos a construir otros objetos sobre la figura. Por ejemplo, podemos trazar las diagonales del hexágono.
[1] Podríamos hacer una segunda construcción aproximada a partir del punto D como punto cualquiera sobre AB: encontrando los puntos F sobre BC y H sobre CA tales que DB=FC=HA. De esta manera el triángulo DFH es equilátero, y podríamos construir también el triángulo EGI equilátero. Así obtendríamos un hexágono equilátero con tres de sus lados sobre ABC, pero no garantizamos que la longitud de sus lados sea PQ.

Inmediatamente constatamos que se cortan en un punto que parece ser el centro (incentro, circuncentro, ortocentro y baricentro) de ABC. Podemos verificar experimentalmente esa conjetura construyendo las mediatrices de ABC.
Ahora bien, teniendo en cuenta las hipótesis experimentales anteriores, podemos afirmar que las diagonales de DEFGHI son mediatrices de los triángulos equiláteros DFH y EGI. Y por lo tanto, forman ángulos de 60° entre ellas[1].
Esta propiedad adicional involucra al punto D, que aún no sabemos construir de manera exacta. En efecto, sabemos que el segmento DE debe estar sobre AB, que DE debe ser igual a PQ y que el ángulo DOE (llamando O al ortocentro del triángulo ABC) debe medir 60°.
¿Existe una manera de garantizar estas tres propiedades?
Intentemos con una nueva construcción aproximada. Teniendo el triángulo ABC, su ortocentro O y el segmento PQ, podemos construir como antes el segmento DE sobre AB, tal que DE=PQ.
[1] Esta es una propiedad de las mediatrices de un triángulo equilátero

¿El ángulo DOE mide 60°? Sabemos que todos los puntos X que son vértices de ángulos DXE que miden 60° están sobre un arco de circunferencia de extremos D y E, y podemos construir ese arco.
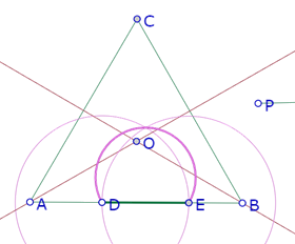
Y podemos mover D de manera que ese arco pase por O.

Pero ¿podemos construir de manera exacta esa posición de D que garantiza que el arco capaz de 60° de extremos D y E pase por O?
Sabemos que al mover D, el arco no cambia de tamaño, simplemente se desplaza siguiendo el movimiento de D. ¿Para cualquier posición de D podemos determinar sobre el arco el punto que coincidirá con O al mover D? Basta con determinar los puntos del arco que están a igual distancia de AB que O. Y esto se logra trazando una paralela a AB por O y construyendo los puntos de intersección con el arco.
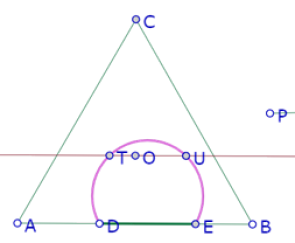
Teniendo esos puntos conocemos la distancia que hay que mover D para que el arco pase por O: será la distancia entre O y uno de los dos puntos de intersección que acabamos de construir.
Para encontrar ese punto podemos entonces construir el paralelogramo DTOD’, que garantiza que TO=DD’[1].
[1] Ya que en todo paralelogramo los lados opuestos son iguales.

Ya sabemos construir de manera exacta el punto D’ que garantiza que D’E’=PQ y <D’OE’=60°. Y teniendo ese punto podemos construir el hexágono D’E’F’G’H’I’, tal como hicimos con la primera construcción aproximada.

Para verificar si es una construcción exacta debemos arrastrar todos los objetos que componen la figura; si las propiedades pedidas se conservan al arrastrar cualquiera de los objetos que componen la figura, es una construcción exacta.
Sabemos que los objetos que pueden arrastrarse son los puntos A, B, P, Q (y D que está oculto). Vamos a mostrar a continuación algunos de los casos que se obtienen al arrastrar esos puntos.

(Después de arrastrar A)
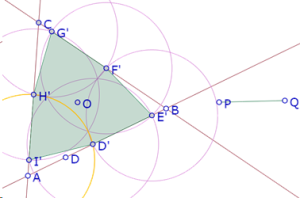
(después de arrastrar B)

(Después de arrastrar D)
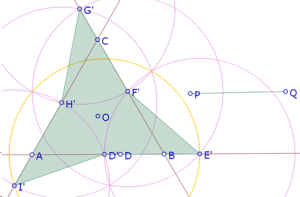
(después de arrastrar Q)
Así que experimentalmente podemos afirmar que la construcción es exacta.
Pero aquí no termina el trabajo en la solución del problema, pues esta construcción se hizo con base en hipótesis de propiedades que deben cumplirse, propiedades que encontramos de manera perceptiva en una construcción aproximada. El rigor matemático nos exige renunciar a toda hipótesis basada únicamente en la percepción. Así que necesitamos dar un fundamento deductivo a las hipótesis que formulamos a partir de la percepción.
Parte II: experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
La construcción exacta que encontramos se basa en las siguientes hipótesis experimentales:
- Los triángulos DFH y EGI son equiláteros.
- Las diagonales del hexágono DEFGHI son mediatrices de los triángulos DFH y GHI.
- Las diagonales del hexágono DEFGHI se cortan en el incentro del triángulo ABC.
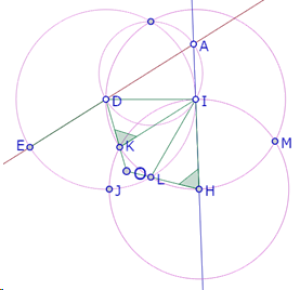
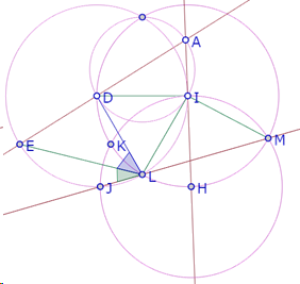
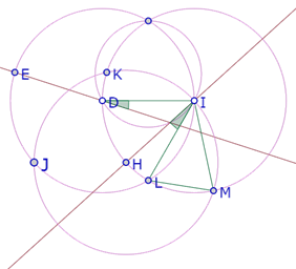
Hagamos una construcción para examinar la relación entre el ángulo de 60° del triángulo ABC y tres lados consecutivos del hexágono DEFGHI.
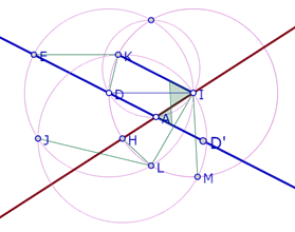
Si partimos del lado ID del hexágono, y sabemos que los lados DE y HI están respectivamente sobre los lados AB y AC del triángulo, debemos construir el punto A de manera que el ángulo DAI=60°.
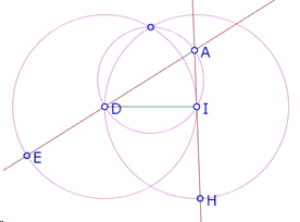
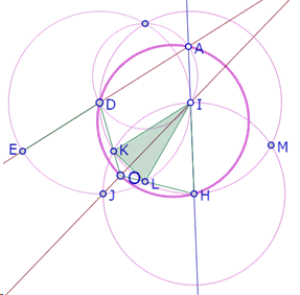
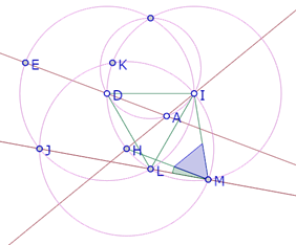
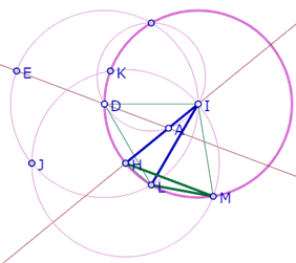
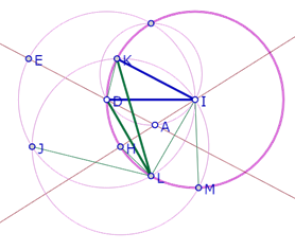
Si construimos el círculo de centro H que pasa por I observamos que tres de los puntos de intersección de los tres círculos congruentes forman un triángulo equilátero.

Y la diagonal HE del hexágono sería mediatriz de ese triángulo, con lo cual podría demostrarse que las diagonales de DEFGHI se cortan en un solo punto y forman ángulos de 60°[1]
[1] En un triángulo equilátero las mediatrices de los lados son también bisectrices de los ángulos. Entonces dos bisectrices forman con el lado común un triángulo isósceles de ángulos 120°, 30°, 30°. Como la tercera bisectriz es mediatriz del lado común, será bisectriz del ángulo opuesto a ese lado que mide 120°. Por eso los ángulos entre las mediatrices de un triángulo equilátero miden 60°.
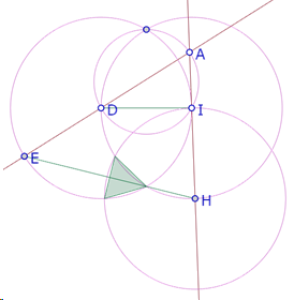
Llamemos J, K y L esos puntos e intentemos deducir del procedimiento de construcción que efectivamente JKL es un triángulo equilátero.

Llamemos M a la segunda intersección del círculo de centro H que pasa por I y el círculo de centro I que pasa por H.

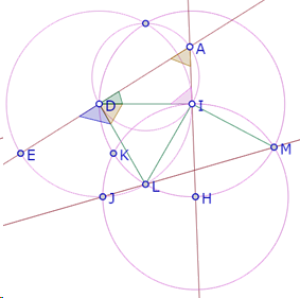
Como el círculo de centro I pasa por H y el círculo de centro H pasa por I, podemos deducir que los triángulos IKH y HIM son equiláteros. Pero el ángulo KHM es la suma de los ángulos KHI y MHI, por lo tanto mide 120°.
Además, el ángulo KHM es el ángulo central correspondiente a la cuerda KM y el ángulo KJM es un ángulo inscrito en el arco mayor definido por esa cuerda. Así que el ángulo KJM mide 60°.
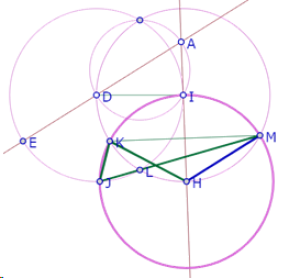
Si demostramos que los puntos J, L, M están alineados[1], queda demostrado que el ángulo KJL mide 60°.
[1] Esta demostración se presenta más adelante
Por otro lado, si consideramos el círculo de centro I que pasa por H, el ángulo KLM está inscrito en el arco menor definido por la cuerda KM, y el ángulo KIM es el ángulo central definido por esa misma cuerda.
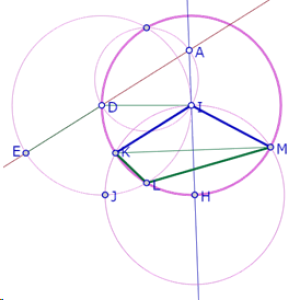
Como el ángulo KIM es la suma de los ángulos KIH y MIH, que son ángulos de triángulos equiláteros, KIM mide 120°. Y el ángulo KLM es suplementario de la mitad del ángulo KIM.
KLM=180-KIM/2=180-60=120
Si demostramos que los puntos J, L, M están alineados, queda demostrado que el ángulo JLK, suplementario del ángulo KLM, mide 60°.
Ahora bien, si el ángulo KJL mide 60° y el ángulo KLJ mide 60°, necesariamente el ángulo LKJ mide 60° y por lo tanto JKL es un triángulo equilátero.
Procedamos a hora a justificar deductivamente que J, L, M están alineados.
El punto L es intersección del círculo de centro D que pasa por I y el círculo de centro I que pasa por D. Por lo tanto el triángulo DIL es equilátero, y el ángulo DLI mide 60°.

Como el ángulo JLM es la suma de los ángulos JLD, DLI e ILM, si deducimos que la suma de los ángulos JLK y MLI es 120°, queda demostrado que el ángulo JLM es llano, por lo tanto J, L, M estarán alineados.
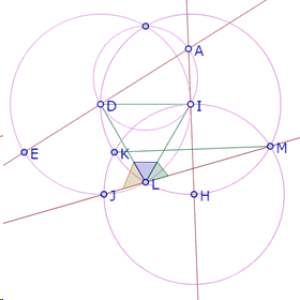
¿Tenemos alguna forma de calcular la medida de los ángulos JLD y MLI?
Como el triángulo LIM es isósceles en I, los ángulos ILM y LMI son iguales.
Pero el ángulo LMI es la resta de los ángulos HMI y HML

Además, el ángulo HMI mide 60° y el ángulo LMH está inscrito en el arco mayor del círculo de centro I definido por la cuerda LH.

Entonces es la mitad del ángulo LIH. Así que el ángulo LMI mide 60° menos la mitad del ángulo LIH.
Por otra parte, la suma de los ángulos HIL, LID (cuya medida es 60°) y DIA es 180°, ya que H, I, A están alineados.
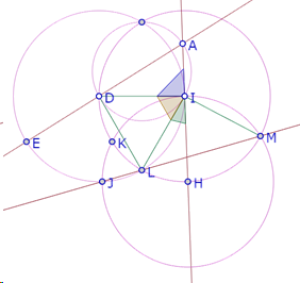
Y la suma de los ángulos DIA, IDA y DAI (cuya medida es 60°) es 180° porque son los ángulos internos del triángulo ADI.
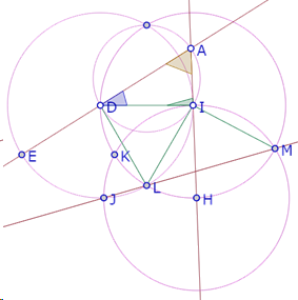
Entonces
< IDA = 180- 60 - <DIA y < HIL=180-60-<DIA, por lo tanto los ángulos HIL e IDA son iguales.
Así que el ángulo MLI mide 60° menos la mitad del ángulo IDA.
Ahora busquemos una forma de calcular la medida del ángulo JLD.
El triángulo JLD es isósceles en D, por lo tanto los ángulos JLD y LJD son iguales.

Diana nos pidió presentar el 14 a las 2:45 para una obra social en el barrio Santafe, detrás del cementerio central
Si demostramos que J está sobre el círculo de centro E que pasa por D[1], entonces quedará demostrado que el ángulo EDJ mide 60°.
[1] Esta demostración se presenta más adelante
Pero el ángulo JLE está inscrito en el arco mayor definido por la cuerda EJ en el círculo de centro D que pasa por E, y tiene como ángulo central a EDJ, por lo tanto el ángulo JLE mide 30°.

Así que <JLD=<JLE+<ELD
<JLD=30+<ELD
<JLD=30+(180-<EDL)/2
Por otra parte, la suma de los ángulos EDL, LDI (que mide 60°) y ADI es 180° porque A, D, E están alineados, y la suma de los ángulos ADI, DAI (que mide 60°) y AID es 180° por ser ángulos interiores del triángulo ADI.
Así que
<EDL = 180-60-<ADI y <AID=180-60-<ADI, por lo tanto los ángulos EDL y AID son iguales.
En conclusión,
<JLD=30+(180-<AID)/2
Ahora podemos calcular la medida de la suma de los ángulos JLD y MLI
<JLD+<MLI= 30+(180-<AID)/2+60-<IDA/2
=30+90-<AID/2+60-<IDA/2
=180- (AID+IDA)/2
=180-(120)/2
=180-60=120.
Y por lo tanto los puntos J, L, M están alineados.
Pero solamente si demostramos que J está sobre el círculo de centro E que pasa por D. Pasemos ahora a buscar una justificación deductiva de esa propiedad.
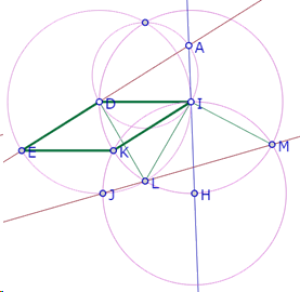
Los ángulos DAI y KIH miden 60° y son ángulos correspondientes entre dos rectas cortadas por una transversal, por lo tanto la recta ED es paralela a la recta KI.

Pero los segmentos ED y KI son iguales por ser radios de círculos congruentes. Por lo tanto, el cuadrilátero EDIK es un paralelogramo.
Pero los segmentos DI y KI son iguales por ser radios de un mismo círculo, así que el cuadrilátero EDIK es un rombo .
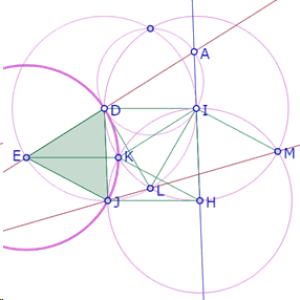
Pero como DI es paralelo a EK (por ser lados opuestos de un paralelogramo) y DI es paralelo a JH (por ser lados opuestos de un paralelogramo), entonces JH es paralelo a EK (por transitividad del paralelismo).
Además, DI=EK (por ser lados de un rombo) y DI=JH (por ser lados de un rombo), así que EK=JH (por transitividad de la igualdad).
Por consiguiente, el cuadrilátero EKHJ es un paralelogramo. Pero JH=HK por ser radios del mismo círculo. Entonces EKHJ es rombo, y EK=EJ=ED

Por lo tanto queda demostrado que ED y EJ son radios del mismo círculo; es decir, que el círculo de centro E que pasa por D también pasa por J.
Por consiguiente el triángulo EJD es equilátero.
Hemos demostrado entonces que como el ángulo DAI mide 60° y los segmentos HI, ID ED son congruentes, entonces el triángulo JKL formado por las intersecciones de los círculos que garantizan que esos segmentos son congruentes, es equilátero.

Como demostramos que el círculo de centro E que pasa por D también pasa por K y por J, si tomamos ahora en consideración el ángulo ABC del triángulo equilátero, que es el mismo ángulo ECF, y los lados ED, EF y FG del hexágono DEFGHI, podemos demostrar usando los mismos argumentos, que la recta DG (diagonal del hexágono) es mediatriz del segmento JL.
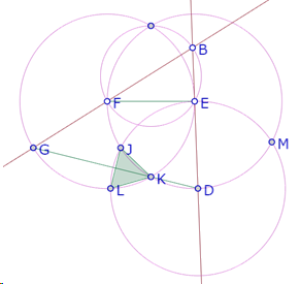
Y si tomamos en consideración el ángulo BCA del triángulo equilátero y los lados FG, GH y HI del hexágono, podemos concluir que la recta FI es mediatriz del segmento KL.

Así que las diagonales del hexágono DEFGHI son mediatrices del triángulo equilátero JKL, de manera que se cortan en un mismo punto y forman entre ellas ángulos de 60°.
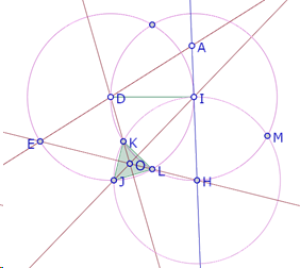
Además queda demostrado que HE, mediatriz de KJ, pasa necesariamente por el punto L[1], DG, mediatriz de JL pasa por el punto K y FI, mediatriz de KL, pasa por el punto J.
[1] Ya que L es equidistante de J y K por ser JKL un triángulo equilátero
Pero como DIKE es un rombo, los puntos D y K equidistan de los puntos E e I. Por lo tanto la recta DK (que es la misma recta DG) es mediatriz del segmento EI.

De la misma forma podemos demostrar que la recta FI es mediatriz del segmento EG y que la recta HE es mediatriz del segmento GI.


Por consiguiente, las mediatrices del triángulo EGI forman ángulos de 60°, y necesariamente EGI es un triángulo equilátero.
Por otra parte, ya demostramos que DIHJ es un rombo, así que J e I equidistan de H y D, y JI (que es la misma recta IF) es mediatriz del segmento HD.

De la misma forma podemos demostrar que la recta HE es mediatriz de DF

y la recta GD es mediatriz de HF
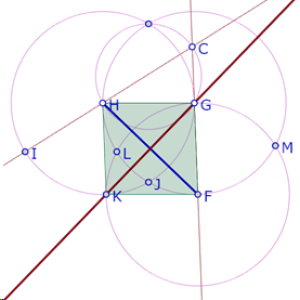
Por consiguiente, las mediatrices del triángulo DFH forman ángulos de 60° y necesariamente DFH es un triángulo equilátero.
Así que ya hemos demostrado las dos primeras hipótesis experimentales en las que se basa nuestra solución del problema de construcción.
Ahora vamos a demostrar que las diagonales del hexágono DEFGHI, que son las mismas mediatrices del triángulo JKL, se cortan en el centro del triángulo ABC.
Podemos utilizar como argumento que O está a igual distancia de AB, BC y CA, para lo cual tendríamos que demostrar que los triángulos AOH y AOD tienen la misma altura.
Pero al considerar esos triángulos, constatamos que los ángulos OAH y OAD miden 30°, así que OA es bisectriz del ángulo ABC.

¿Cómo demostrar que efectivamente OAH y OAD miden 30°?
Si O, A, H, D están sobre un mismo círculo y OH=OD, necesariamente los ángulos OAH y OAD son iguales.
Vamos a intentar justificar deductivamente esas dos propiedades.
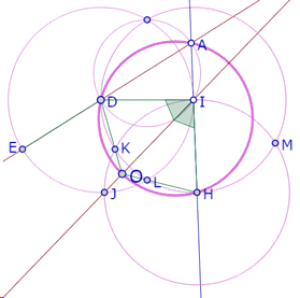
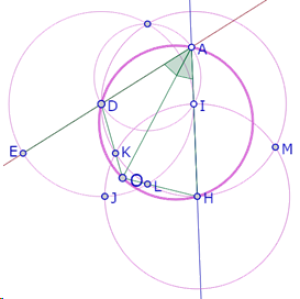
Retomemos nuestra construcción inicial, con el ángulo DAI y los lados HI, ID, DE del hexágono. Llamemos O al punto de intersección de las mediatrices del triángulo JKL
Los triángulos ILH e IKD son isósceles, porque HI, LI, KI, DI son radios del mismo círculo.

Pero ya hemos demostrado que el ángulo HIL es igual al ángulo IDA y que DA es paralela a KI. Como los ángulos KID y ADI son ángulos alternos internos formados por la transversal DI con las rectas DA y KI, entonces son ángulos iguales.
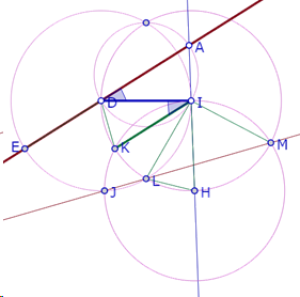
Por lo tanto, los ángulos DIK y LIH son iguales, y por consiguiente los triángulos DIK y LIH son congruentes.
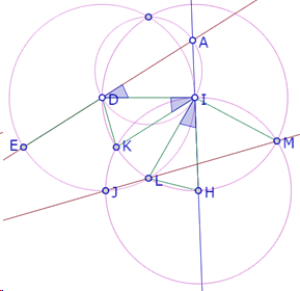
Consideremos ahora el cuadrilátero AHOD.
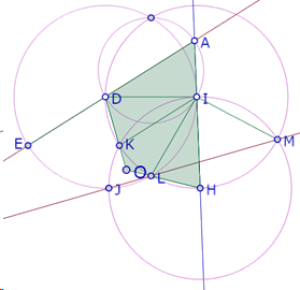
Como el triángulo DIH es isósceles, entonces la recta IO es también mediatriz de DH y por lo tanto contiene el centro O’ del círculo que pasa por D, A, H, O[1]
[1] Ya que la mediatriz de un segmento contiene todos los puntos que equidistan de los extremos del segmento, y O’ por ser centro del círculo que pasa por D y por H, equidista de esos dos puntos.

Pero el triángulo DO’H es isósceles en O’, así que la recta JO (mediatriz del segmento DH) es bisectriz del ángulo DO’H.
Por consiguiente, el ángulo DO’O es la mitad del ángulo DO’H y el ángulo OO’H es la mitad del ángulo DO’H.
Pero el ángulo DAO está inscrito en el arco mayor definido por la cuerda DO y cuyo ángulo central es DO’O. Por lo tanto el ángulo DAO es la mitad del ángulo DO’O.
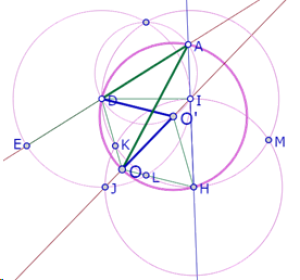
Por otra parte, el ángulo HAO está inscrito en el arco mayor definido por la cuerda OH, cuyo ángulo central es OO’H, que es igual al ángulo DO’O.
Por lo tanto el ángulo HAO es la mitad del ángulo HO’O
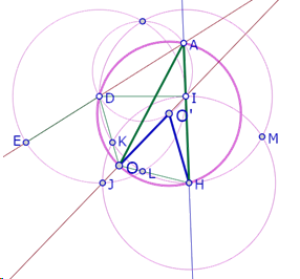
Como los ángulos HO’O y DO’O son iguales, necesariamente los ángulos DAO y HAO también son iguales
Por consiguiente, O está sobre la bisectriz del ángulo DAH, que es el mismo ángulo DAI (y el mismo ángulo BAC del triángulo equilátero).
De la misma manera podemos demostrar que O está sobre la bisectriz del ángulo ABC, y sobre la bisectriz del ángulo BCA, y por lo tanto es el incentro del triángulo ABC.
Hasta aquí hemos demostrado las tres hipótesis experimentales que están a la base de la solución del problema de construcción, pero únicamente para el caso en el que el segmento AB/3<PQ<AB/2, y el hexágono ‘está en el interior’ del triángulo ABC.
Es necesario considerar el caso en el que PQ>AB/2 y el hexágono ‘sale’ del triángulo ABC.
Vamos a seguir el mismo camino que para el primer caso: demostrar que el triángulo JKL es equilátero, y que las diagonales del hexágono son mediatrices de ese triángulo, para concluir que se cortan en un punto y forman ángulos de 60°. Luego demostraremos que el incentro de JKL es también incentro de ABC.
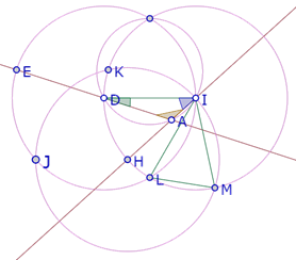
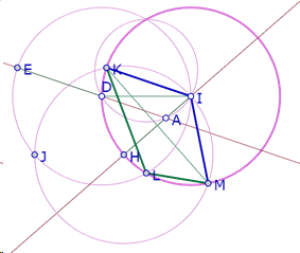
Comanzamos con la construcción del ángulo DAI de 120° y los lados HI, ID y DE del hexágono regular.
En este caso A está en el arco menor definido por la cuerda DI, cuyo ángulo central es de 120°, para garantizar que el ángulo DAI mide 120°.

Llamamos J, K, L las intersecciones de los tres círculos congruentes, y M la segunda intersección del círculo de centro I que pasa por H y el círculo de centro H que pasa por I.

Como los triángulos IHK e IHM son equiláteros, el ángulo KHM mide 120°.
Pero el punto J está sobre el arco mayor definido por la cuerda KM, así que el ángulo KJM mide la mitad del ángulo KHM, es decir 60°.
Si demostramos que J, L, M están alineados, quedará demostrado que el ángulo KJL mide 60°

Por otra parte, el ángulo KLM está inscrito en el arco menor definido por la cuerda KM, cuyo ángulo central KIM mide 120°. Entonces el ángulo KLM es suplementario de la mitad del ángulo KIM, es decir mide 120°.
Si demostramos que J, L, M están alineados, podremos deducir que el ángulo JLK mide 60°, ya que es suplementario del ángulo KLM.
Y así quedaría demostrado que el triángulo KLM es equilátero, ya que tendría dos ángulos de 60°.
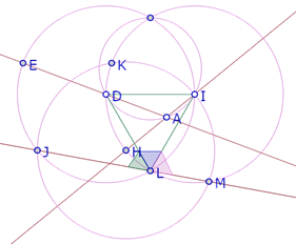
Ahora vamos a deducir que J, L, M están alineados.
Como el ángulo JLM es la suma de los ángulos JLD, DLI (que mide 60°), ILM, si demostramos que la suma de JLD e ILM es 120° quedará demostrado que JLM es un ángulo llano y por lo tanto J, L, M están alineados.
Ahora bien, el triángulo ILM es isósceles en I, por lo cual los ángulos ILM e IML son iguales.
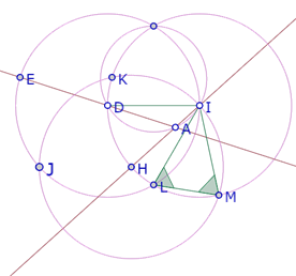
Pero el ángulo IML es la suma de los ángulos IMH y HML
Además, el ángulo HLM está inscrito en el arco mayor definido por la cuerda HL cuyo ángulo central es HIL
Por otra parte, el ángulo HIL es la resta de los ángulos LID (que mide 60°) y AID

Así que <IDA=60°- <AID y <LIH=60°-<AID, por consiguiente los ángulos LIH e IDA son iguales.
Entonces la medida del ángulo HML es la mitad del ángulo IDA y <MLI=60+<IDA/2.
Ahora calculemos la medida del ángulo JLD.
El ángulo JLD es la resta de los ángulos JLK (que mide 60°) y DLK.

Por otra parte, el ángulo DLK está inscrito en el arco mayor definido por la cuerda KD, cuyo ángulo central es DIK
Además, el ángulo KIH mide 60° porque el triángulo KIH es equilátero. Y el ángulo IAD’ es suplementario del ángulo DAI que mide 120°. Como AI es una transversal de las rectas DA y KI, y los ángulos IAD’ y HIK son alternos internos e iguales, entonces las rectas KI y DA son paralelas.
Por lo tanto, los ángulos KID y ADI que son alternos internos son iguales.

Por consiguiente, el ángulo DLK es la mitad del ángulo ADI.
Ahora, si calculamos la suma de los ángulos JLD y MLI, tenemos:
<JLD+<MLI=(60-IDA/2)+(60+IDA/2)=120°
Así queda demostrado que J, L, M están alineados, ya que la suma de los ángulos JLD, DLI y MLI es 180°.
Ahora vamos a demostrar que el círculo de centro E que pasa por D también pasa por K y por L.
Ya demostramos que KI es paralelo a ED. Pero además KI=ED (por ser radios de círculos congruentes), por consiguiente KIDE es paralelogramo.
Pero KI=DI (por ser radios del mismo círculo), así que KIDE es rombo y por lo tanto EK=ED.
Por consiguiente EK es paralelo a JH (por transitividad del paralelismo) y EK=JH (por transitividad de la igualdad. Entonces EKHJ es paralelogramo.
Pero HK=HJ (por ser radios del mismo círculo), por consiguiente EKHJ es rombo y EK=EJ.
Así que el círculo de centro E que pasa por D, pasa también por K y por J.

Ya demostramos que el triángulo JKL es equilátero.
Ahora bien, ya demostramos que EK=EJ y HK=HJ, así que la recta EH es mediatriz del segmento JK.

Como demostramos que el círculo de centro E que pasa por D también pasa por K y por J, si tomamos ahora en consideración el ángulo ABC del triángulo equilátero, que es el mismo ángulo EBF, y los lados DE, EF y FG del hexágono DEFGHI, podemos demostrar usando los mismos argumentos, que la recta DG (diagonal del hexágono) es mediatriz del segmento JL.
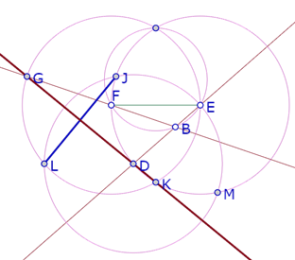
Y si tomamos en consideración el ángulo BCA del triángulo equilátero y los lados FG, GH y HI del hexágono, podemos concluir que la recta FI es mediatriz del segmento KL.
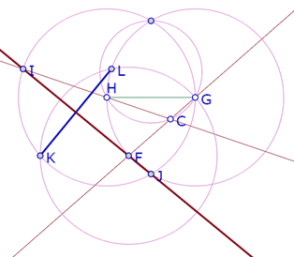
Así que las diagonales del hexágono DEFGHI son mediatrices del triángulo equilátero JKL, de manera que se cortan en un mismo punto y forman entre ellas ángulos de 60°. Además queda demostrado que HL, mediatriz de KJ, pasa necesariamente por el punto L, DG, mediatriz de JL pasa por el punto K y FI, mediatriz de KL, pasa por el punto J.
Pero como DIKE es un rombo, los puntos E e I equidistan de los puntos D y K. Por lo tanto la recta DK (que es la misma recta DG) es mediatriz del segmento EI.

De la misma forma podemos demostrar que la recta FI es mediatriz del segmento EG

y que la recta HE es mediatriz del segmento GI

Por consiguiente, las mediatrices del triángulo EGI forman ángulos de 60°, y necesariamente EGI es un triángulo equilátero.
Por otra parte, ya demostramos que DIHJ es un rombo, así que J e I equidistan de H y D, y JI (que es la misma recta IF) es mediatriz del segmento HD.
De la misma forma podemos demostrar que la recta HE es mediatriz de DF y la recta GD es mediatriz de HF. Por consiguiente, las mediatrices del triángulo DFH forman ángulos de 60° y necesariamente DFH es un triángulo equilátero.
Así que ya hemos demostrado las dos primeras hipótesis experimentales en las que se basa nuestra solución del problema de construcción.
Ahora vamos a demostrar que las diagonales del hexágono DEFGHI, que son las mismas mediatrices del triángulo JKL, se cortan en el incentro del triángulo ABC.
Retomemos nuestra construcción inicial, con el ángulo DAI y los lados HI, ID, DE del hexágono. Llamemos O al punto de intersección de las mediatrices del triángulo JKL

Consideremos el cuadrilátero DAHO.
El ángulo DAH es suplementario del ángulo DAI, por lo tanto mide 60°. El ángulo DOH mide 120°. Por lo tanto DAH y DOH son suplementarios.

Ahora comparemos los otros ángulos opuestos del cuadrilátero
El ángulo AHO es suplementario del ángulo IHL.

Pero los triángulos HIL y KID son congruentes, por lo que <IHL=<IDK.
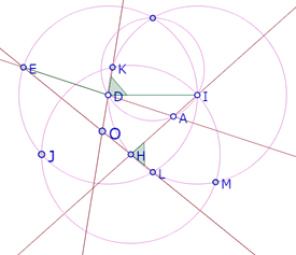
Por consiguiente el ángulo AHO es suplementario del ángulo IDK.

Pero IK es paralelo a DA, así que el ángulo IKD (que es igual al ángulo IDK) es igual al ángulo ADO. Por lo tanto los ángulos AHO y ADO son suplementarios.
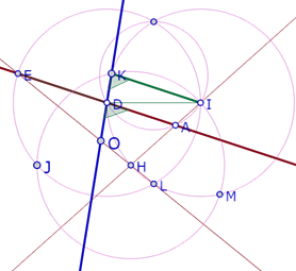
Así que el cuadrilátero DAHO es cocíclico

Ahora bien, como el triángulo IKL es isósceles en I, la recta IJ, que pasa por O y es mediatriz de KL, también es bisectriz del ángulo KIL.

Pero ya demostramos que los ángulos DIK y LIH son iguales, por lo tanto podemos concluir que IO es bisectriz del ángulo DIH[1].
[1] <KIO-<KID=<LIO-<LIH
Pero el triángulo DIH es isósceles en I, así que la recta IO es mediatriz del segmento DH.
Por consiguiente, la recta IO pasa por el centro O’ del círculo que pasa por D, A, H, O[1].
[1] Porque la mediatriz de un segmento contiene todos los puntos que equidistan de los extremos del segmento, y el punto O’ por ser centro del circulo que pasa por D y H, equidista de esos puntos.

Pero el ángulo DAO está inscrito en el arco mayor definido por la cuerda DO cuyo ángulo central es DO’O. Por lo tanto el ángulo DAO es la mitad del ángulo DO’O.
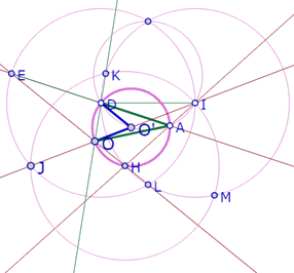
Pero el ángulo HAO está inscrito en el arco mayor definido por la cuerda OH, cuyo ángulo central es OO’H, que es igual al ángulo DO’O. Por lo tanto el ángulo HAO es igual al ángulo DAO.

Por consiguiente, O está sobre la bisectriz del ángulo DAH, que es el mismo ángulo DAI (y el mismo ángulo BAC del triángulo equilátero).

De la misma manera podemos demostrar que O está sobre la bisectriz del ángulo ABC, y sobre la bisectriz del ángulo BCA, y por lo tanto es el incentro del triángulo ABC.
Así terminamos la demostración de las tres hipótesis experimentales de nuestra solución del problema, para el caso en el que el ángulo DAI mide 120°.