Primer ejemplo
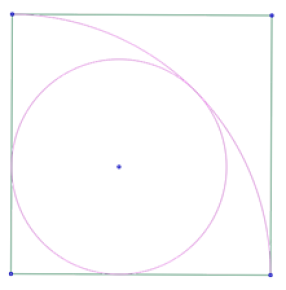
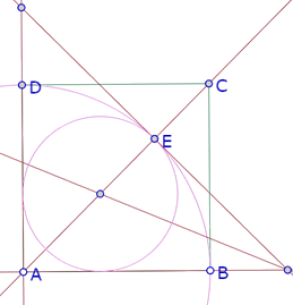
Se trata de reproducir esta imagen, donde puede identificarse un cuadrado, un arco que es un cuarto del círculo con centro en un vértice del cuadrado y que pasa por un vértice consecutivo, y un círculo tangente a ese arco y a dos lados adyacentes del cuadrado.
Parte I: experimentación para encontrar una construcción exacta
Comencemos con una construcción aproximada, a partir de un cuadrado y un círculo.
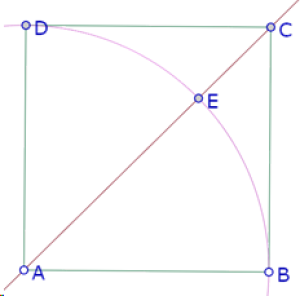
Como el círculo interior debe ser tangente a AB y AD, su centro debe estar sobre la bisectriz del ángulo BAD. Y el punto de tangencia de los dos círculos debe ser la intersección de esa bisectriz con el círculo de centro A que pasa por B.
Colocamos un punto O sobre la bisectriz del ángulo BAD y construimos el círculo de centro O que pasa por E.
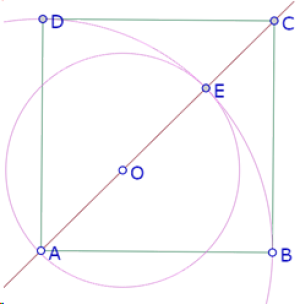
Luego acomodamos la posición de O para hacer que el círculo parezca tangente a AB y AD.
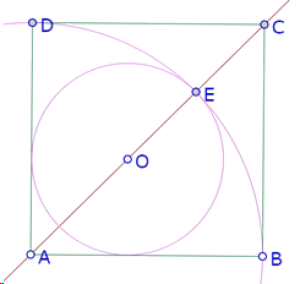
En esa posición, parece cumplirse que OE=EC. Y esa propiedad sería un medio de construir O de manera exacta.
Así que vamos a hacer una verificación experimental construyendo O como simétrico de C con respecto a E.
Al construir el círculo de centro O que pasa por E, parece ser tangente a AB y AD.
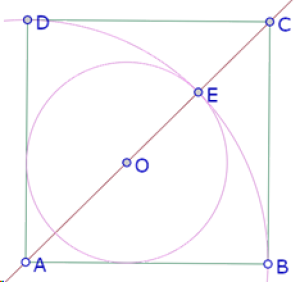
Pero la percepción no es suficiente para verificar la tangencia, así que vamos a construir una recta perpendicular a AB por O, el punto F de intersección de esa recta con el círculo de centro O que pasa por E y medimos el ángulo OFA.
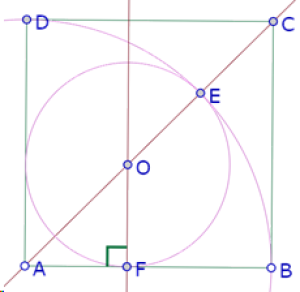
Como el ángulo AFO es recto, el círculo es tangente a AB. Y como O está sobre la bisectriz de BAD, necesariamente es tangente también a AD.
Pero aquí no termina el trabajo en la solución del problema, pues esta construcción se hizo con base en hipótesis de propiedades que deben cumplirse, propiedades que encontramos de manera perceptiva en una construcción aproximada. El rigor matemático nos exige renunciar a toda hipótesis basada únicamente en la percepción. Así que necesitamos dar un fundamento deductivo a las hipótesis que formulamos a partir de la percepción.
Parte II: experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
Ahora debemos buscar una justificación deductiva de la conjetura experimental que está a la base de la solución propuesta: OE=EC.
Si el círculo de centro O que pasa por E es tangente al círculo de centro A que pasa por B y al lado AB, necesariamente EO=OF.
Además, el triángulo AFO es rectángulo en F. Pero como AC es bisectriz del ángulo recto BAD, el ángulo FAO mide 45°, así que AFO es un triángulo isósceles y por consiguiente AF=OF=OE.
Intentemos ahora considerar triángulos que nos permitan poner en relación los segmentos CE y OE.
Si trazamos una perpendicular a AB por E, su intersección con AB genera otro triángulo rectángulo isósceles (AGE).
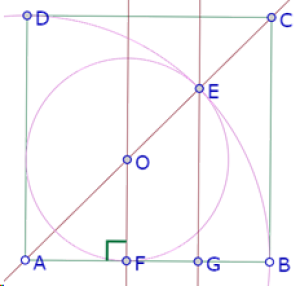
Tenemos entonces tres triángulos rectángulos isósceles, que por lo tanto son semejantes: AFO, AGE y ABC.
Por las condiciones del problema sabemos que AE=AB, OE=AE-AO y EC=AC-AE.
Es decir, tenemos tres triángulos isósceles rectángulos, relacionados entre ellos porque la hipotenusa de uno es igual a la hipotenusa de otro más su lado, y es además el lado del tercero. Estas condiciones deberían producir necesariamente que la diferencia de las hipotenusas del primero y el segundo sea igual a la diferencia de las hipotenusas del segundo y el tercero.
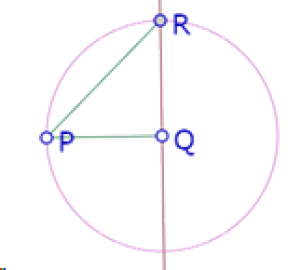
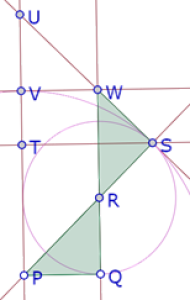
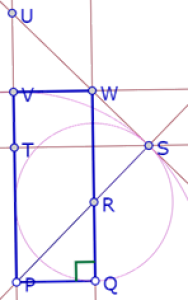
Ahora el segundo triángulo, cuya hipotenusa debe ser PR+QR.
Trazamos la recta PR, el círculo de centro R que pasa por Q y su intersección (S) con la recta PR. Finalmente la paralela a PQ por S y la paralela a RQ por P.
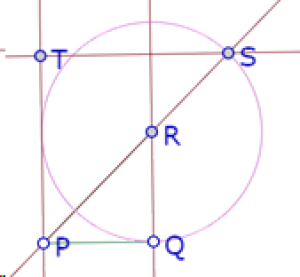
El triángulo PTS cumple esa condición.
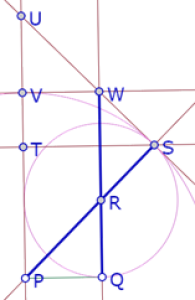
Finalmente un tercer triángulo, cuyo cateto es PS. Construimos la perpendicular a PS por S y su intersección (U) con la recta PT.
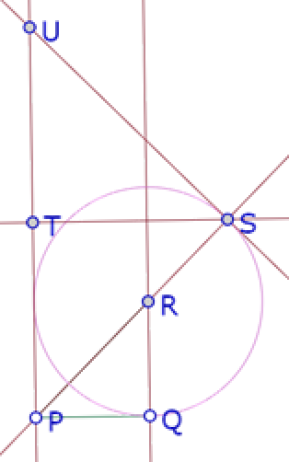
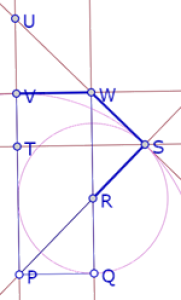
Ya tenemos los tres triángulos, donde el segmento RS es la diferencia de las hipotenusas de los dos primeros. Pero nos falta la diferencia de las hipotenusas del segundo y el tercero. Construimos entonces el círculo de centro P que pasa por S y su intersección (V) con UP.
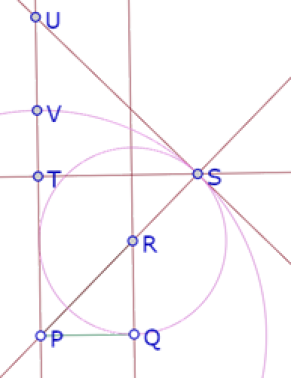
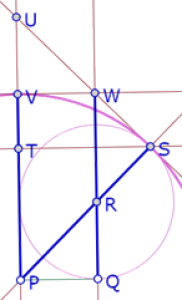
Buscamos entonces argumentos deductivos para justificar que UV=RS.
Sabemos que SU es perpendicular PS y PS es un radio del círculo de centro P que pasa por S, así que US es tangente a ese círculo.
Si consideramos el punto de intersección (W) de QR y US
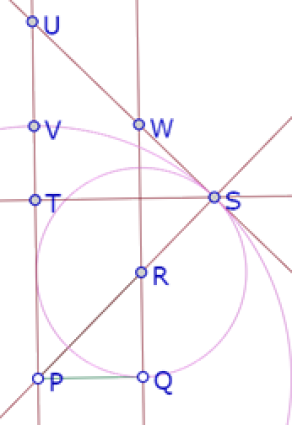
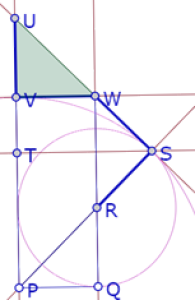
Tendríamos un argumento si logramos mostrar que VW es tangente al círculo de centro O que pasa por S, ya que WS y VW serían tangentes al mismo círculo con un punto en común y por lo tanto serían iguales; además, el triángulo UVW sería isósceles en V, por lo que UV=VW.
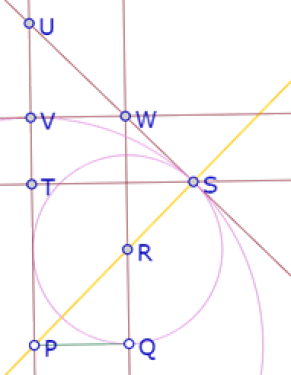
Tenemos que demostrar que VW es perpendicular a UP.
Podemos hacerlo demostrando que PQWV es un rectángulo.
Sabemos que PS=PV por construcción.
Además los triángulos PQR y RSW son congruentes, ya que por construcción RQ=RS.
Eso implica que RW=PR y por lo tanto PS=WQ, ya que PS=PR+RS y WQ=WR+RQ.
Por consiguiente, WQ=PV.
Además, WQ es perpendicular a PQ por construcción y VP es perpendicular a PQ[1]
Lo cual implica que VP es paralela a WQ y como además son iguales, PQWV es un paralelogramo.
Pero como el ángulo PQR es recto, ese paralelogramo es rectángulo.
De manera que VW es perpendicular a PV, por lo tanto VW es tangente al círculo de centro P que pasa por S, y VW=WS=RS.
Pero UVW es rectángulo isósceles en V, por lo que VW=UV
Así queda demostrado que UV=RS.
De manera que si se tienen tres triángulos rectángulos isósceles tales que la diferencia entre las hipotenusas del segundo y el primero es un lado del primero, y la hipotenusa del segundo es un lado del tercero, necesariamente la diferencia entre las hipotenusas del tercero y el segundo es igual a la diferencia de las hipotenusas del segundo y el primero.
En el caso de nuestra construcción,
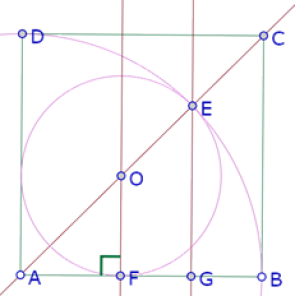
Los triángulos AFO, AGF y ABC son rectángulos isósceles, OE=OF, AE=AB. Por lo tanto EC=EO.
Y así queda demostrada la conjetura experimental que sirvió para construir la solución del problema.
Segunda solución, encontrada deductivamente
Pero también es posible encontrar una solución directamente de manera deductiva:
Como los dos círculos son tangentes, tienen una recta tangente común en el punto de tangencia: la recta perpendicular al radio común.
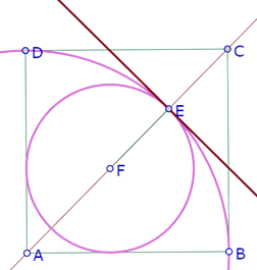
De manera que el círculo interior es en realidad el incírculo de las rectas AB, AD y la perpendicular a AC por E.
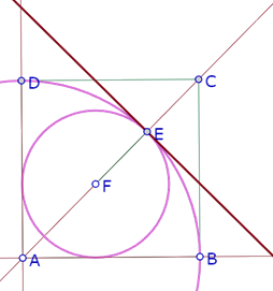
Es decir, es el problema de construir el incírculo de un triángulo, problema que sabemos resolver, pues el centro de ese círculo es la intersección de las bisectrices de los ángulos.
