Tercer ejemplo
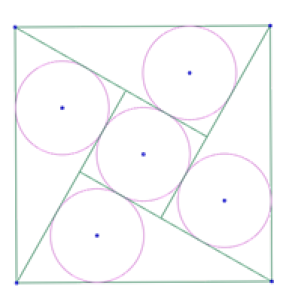
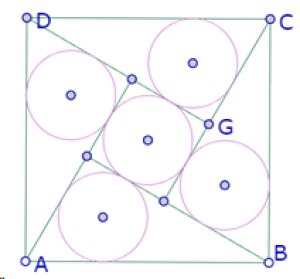
En esta imagen puede verse un cuadrado ‘exterior’, un cuadrado ‘interior’, y cuatro triángulos rectángulos congruentes cuyas hipotenusas son los lados del cuadrado ‘exterior’. Cada triángulo con su incírculo, y el cuadrado interior también con su incírculo. Los cinco círculos son congruentes.
Primera solución
Parte I: experimentación para encontrar una construcción exacta
Comenzamos con una construcción aproximada a partir del cuadrado ‘exterior’.

Para construir los triángulos rectángulos trazamos una recta desde el vértice A hasta un punto sobre el lado DC.
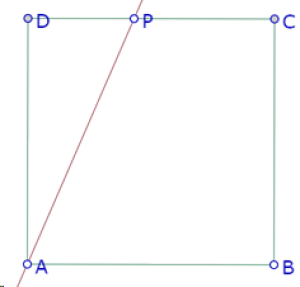
Y luego una paralela a esa recta por el vértice C, y dos perpendiculares a esa recta por los vértices B y D.
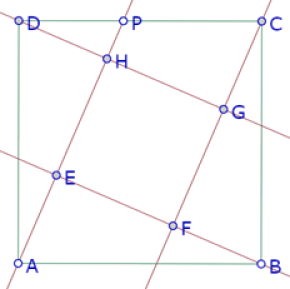
Las intersecciones de esas rectas son a la vez vértices del cuadrado interior y de los triángulos rectángulos ABE, BCF, CDG y DAH.
Finalmente construimos los incírculos de los 5 polígonos interiores
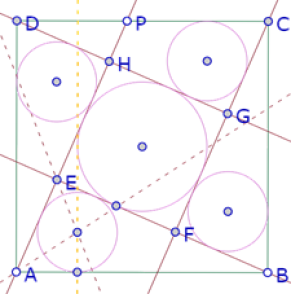
Como puede verse, los círculos no son todos congruentes. Para obtener esa propiedad, es necesario ajustar la posición de P.
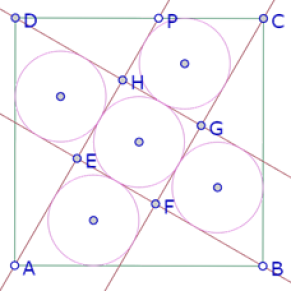
Ahora podemos ver que cada incírculo exterior es tangente a tres rectas y un lado del cuadrado exterior.
Necesitamos determinar la posición del punto P que garantiza esas propiedades.
Una primera pista es buscar si esa posición de P define una razón conocida entre los segmentos DP, PC y DC.
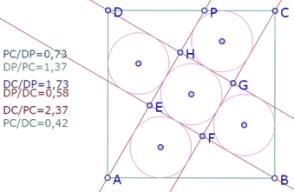
No parecen ser razones notables.
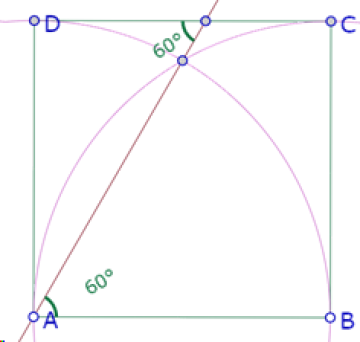
Una segunda pista es examinar los ángulos que forma la recta AP con los lados AD y DC.

Estos sí parecen ser ángulos notables. Sin embargo, no debemos olvidar que esta es una construcción aproximada, y por lo tanto estas medidas también son aproximadas. Los ángulos podrían no medir exactamente 30° y 60°.
Pero podemos verificar utilizando esos ángulos para hacer la construcción y probando si se cumplen las otras propiedades.
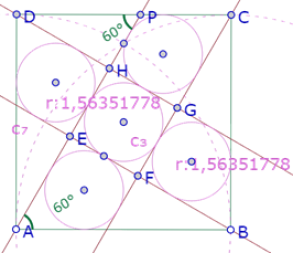
Efectivamente, el hecho de que el ángulo DPA mida 60° garantiza que los cinco círculos sean congruentes[1].
Tenemos entonces una construcción exacta.
Sin embargo, debemos justificar deductivamente la conjetura experimental que llevó a la solución del problema: Si el triángulo ABE es 30-60-90, entonces el incírculo de ABE tendrá el mismo radio del incírculo de EFGH.
[1] En la imagen se muestra la medida de los radios de los círculos c7 (incírculo de ADH) y c3 (incírculo del cuadrado interior) y puede constatarse que son idénticas hasta 8 decimales, que es la máxima precisión en dgpad.
Parte II: Experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
Para esta segunda experimentación, vamos a hacer una construcción de un triángulo rectángulo ABE cualquiera (que corresponde a uno de los triángulos interiores del cuadrado).
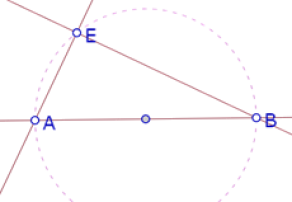
Y luego el triángulo congruente BCF. Sabemos que F está sobre BE y que AE=BF. Así que construimos el círculo de centro B y radio AE que corta BE en el punto F y por ese punto trazamos una perpendicular a BE y una perpendicular a AB por B. Estas dos rectas se cortan en el punto C
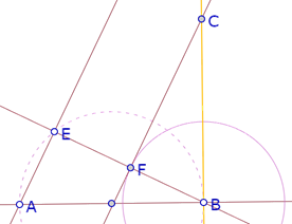
Sabemos que para obtener la solución, el incírculo del triángulo ABE debe ser tangente a la recta FC.
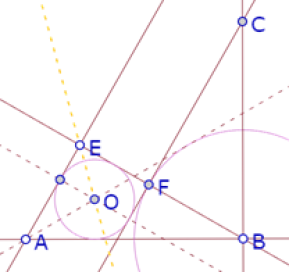
Sabemos que O, al ser punto de intersección de las bisectrices de los ángulos AEB y EAB equidista de las rectas AE, EB y AB. Si además el incírculo es tangente a FC, O debe equidistar de EB (EF) y FC, por lo que debe estar sobre la bisectriz del ángulo EFK. |
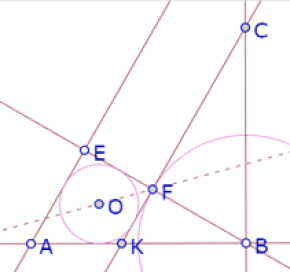
Como el ángulo EFK es un ángulo recto, entonces el ángulo EFO debe medir 45°. Pero el ángulo FEO mide 45°. Así que el triángulo EOF es isósceles en O, y por lo tanto EO=OF.

Por otra parte, FC es perpendicular a EB y BC es perpendicular a AB. Por lo tanto, la bisectriz de EAB es perpendicular a la bisectriz de FBC. Sean I el punto de intersección de esas dos bisectrices, y J el punto de intersección de la bisectriz del ángulo FBC y la recta AE.
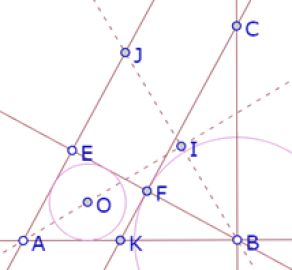
El triángulo ABJ es isósceles, ya que BJ es perpendicular a AI y AI es bisectriz del ángulo BAJ. (Esto se cumple independientemente de que el incírculo de ABE sea tangente A CF)
Pero el ángulo JEB es recto, e I es el punto medio de BJ, así que el círculo de diámetro BJ debe pasar por E. (Esto se cumple independientemente de que el incírculo de ABE sea tangente A CF)
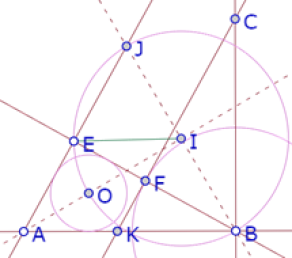
Por consiguiente, IE=IB (Esto se cumple independientemente de que el incírculo de ABE sea tangente A CF)
Ahora bien, (si el incírculo de ABE es tangente a FC) el circulo de centro O que pasa por E también pasa por F, y el círculo de centro B y radio AE también pasa por F. Entonces esos dos círculos tienen un segundo punto de intersección.
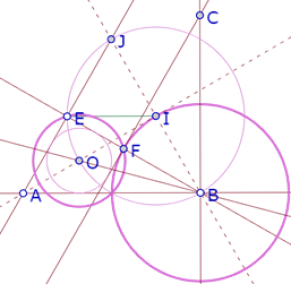
Pero como OB es bisectriz del ángulo ABE, entonces es eje de simetría de las rectas BE y AB. Por consiguiente, ese segundo punto de intersección de los dos círculos, que es el simétrico de F con respecto a OB, debe estar sobre la recta AB.
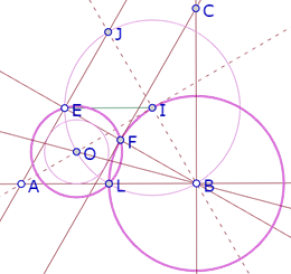
Pero EO=OL, y AO es eje de simetría de AL y AE, así que E y L son simétricos con respecto a AO, de manera que el triángulo EAL es isósceles, con AE=AL.
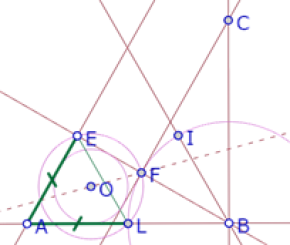
Pero BL=BF que por construcción es igual a AE. Por consiguiente, AL=BL y L es punto medio de AB.
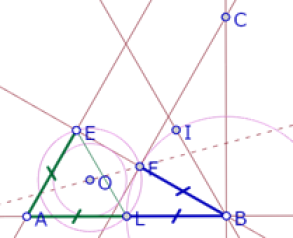
Por consiguiente, AB=2AE y AEB es un ángulo recto, por lo que el triángulo AEB es un triángulo 30-60-90. Que es lo que queríamos demostrar.
Segunda solución
Parte I: Experimentación para encontrar la construcción exacta
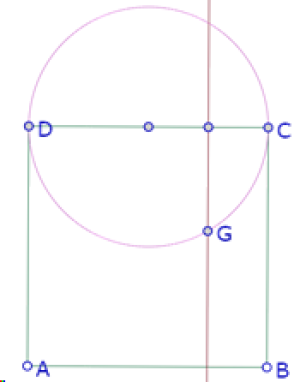
Otra posibilidad de construcción aproximada de este problema es partir de la construcción de uno de los triángulos rectángulos, por ejemplo, colocando un punto P sobre el círculo de diámetro CD.
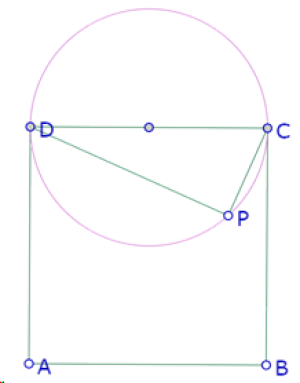
El triángulo cuya hipotenusa es AB, debe ser simétrico del triángulo DPC con respecto al centro del cuadrado.
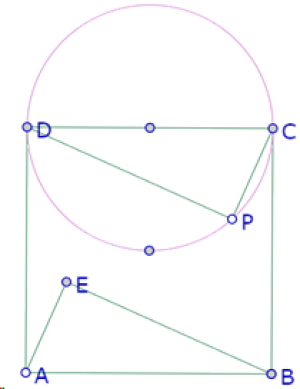
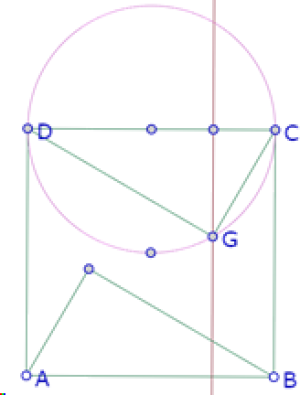
Para construir los otros dos triángulos basta con prolongar los segmentos AE y CP
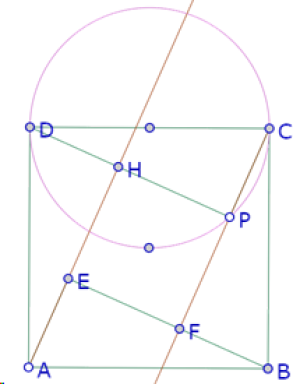
Y finalmente construir los incírculos de los polígonos interiores.
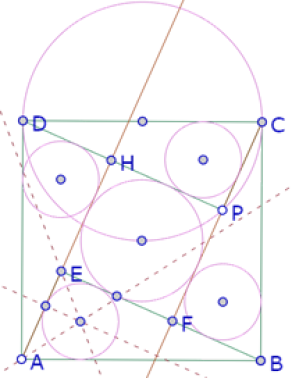
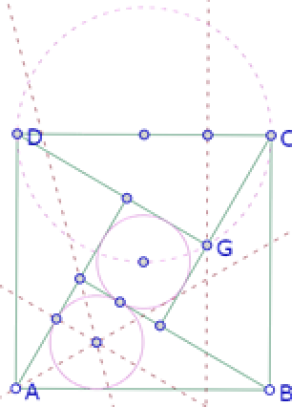
Al igual que para la primera construcción aproximada, para lograr que los cinco círculos sean congruentes, es necesario ajustar la posición del punto P.
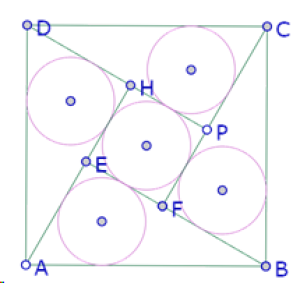
Se trata entonces de determinar la posición exacta de P sobre el círculo de diámetro DC.
Al igual que en la primera experimentación, podemos investigar si hay una relación de proporcionalidad entre el punto P y el segmento DC. Para lo cual construimos la perpendicular a DC por P y el punto P’ de intersección de esa perpendicular con DC.
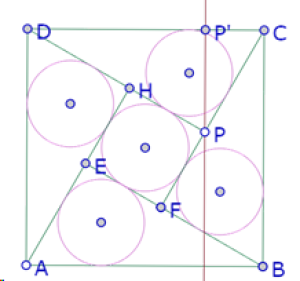
Para verificar si el segmento P’C cabe un número entero de veces en el segmento DC, podemos utilizar la herramienta simetría central (de C con respecto de P’, etc.).

Efectivamente, parece ser que P’C es la cuarta parte del segmento P’C.
Intentemos hacer una construcción con esta conjetura experimental.
Finalmente, verificamos que esos dos círculos tengan el mismo radio
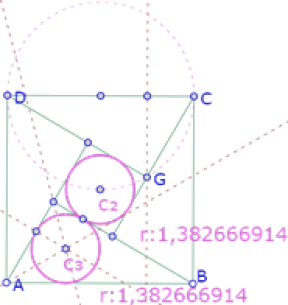
Efectivamente, los círculos tienen el mismo radio, así que tenemos una construcción exacta.
Parte II: Experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
Para justificar deductivamente que si la recta perpendicular a DC que pasa por G corta DC en su cuarta parte la figura es solución, vamos a relacionar un triángulo rectángulo en el que la altura correspondiente a la hipotenusa divide la hipotenusa en una razón 3:1, con un triángulo 30-60-90, del cual hemos ya demostrado que produce una construcción exacta.

En esta figura, DK:KC::3:1
Como sabemos por el teorema de Euclides, GK es la media geométrica de KC y KD. Es decir,
Pero
Por lo tanto,
Por otra parte,
Es decir,
Así que
y por lo tanto GC=2k. Es decir, GC=2KC.
Pero el triángulo DGC es semejante al triángulo GKC, por consiguiente DC=2GC, y DGC es un triángulo 30-60-90.