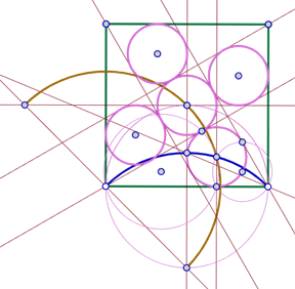
Quinto ejemplo
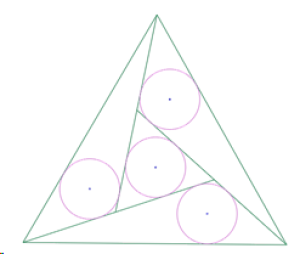
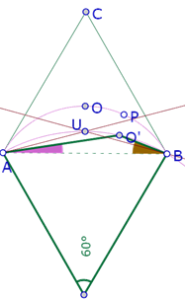
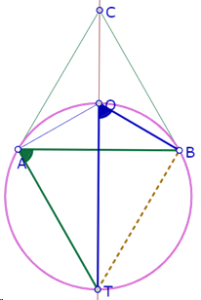
Se trata de reproducir esta imagen en la que puede verse un triángulo equilátero con cuatro triángulos en su interior, cada uno de esos triángulos con sus incírculos[1] que son del mismo radio. Tres de esos triángulos tienen un lado en común con el triángulo equilátero ‘exterior’, y el cuarto triángulo es equilátero y tiene su centro en el centro del triángulo ‘exterior’.
[1] Llamamos incírculo al círculo inscrito dentro de un polígono, es decir que está en el interior del polígono y es tangente a sus lados.
Parte I: experimentación para encontrar una construcción exacta
Comencemos con una construcción aproximada, que parte del triángulo equilátero ‘exterior’.
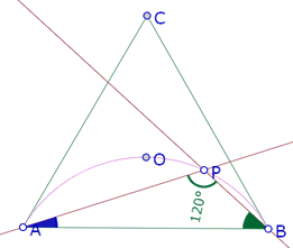
Para construir los triángulos interiores hacemos una primera deducción: Como el triángulo central es equilátero, y sus lados se prolongan hasta los vértices del triángulo exterior, los ángulos formados por los lados de los otros triángulos serán de 120°.
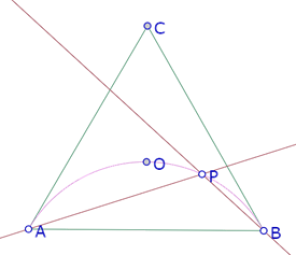
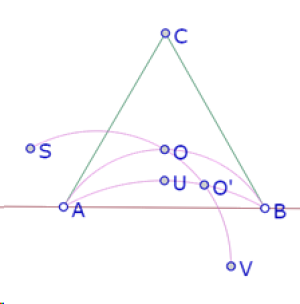
Sabemos que todos los ángulos AXB que miden 120° están sobre un arco de círculo que pasa por el centro del triángulo equilátero ABC.
Así que construimos ese arco, y colocamos un punto sobre él.

Ahora construimos las rectas AP y PB que forman ángulos de 120°.
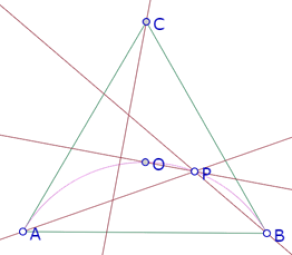
Como P es un vértice del triángulo equilátero ‘interior’, que tiene su centro en O, la recta PO es una altura de ese triángulo, de manera que puede construirse el lado faltante como una recta perpendicular a OP por C.
Finalmente, podemos construir los incírculos de los cuatro triángulos interiores.
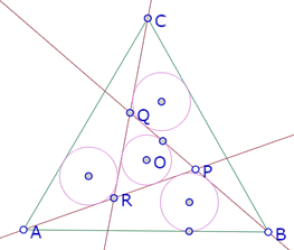
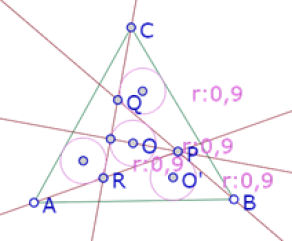
En esta imagen puede verse a simple vista que el incírculo del triángulo PQR es más pequeño que los otros tres, por lo que esta no es una construcción exacta. Podemos acomodar la posición de P sobre el arco hasta lograr que perceptivamente todos los círculos sean del mismo tamaño.
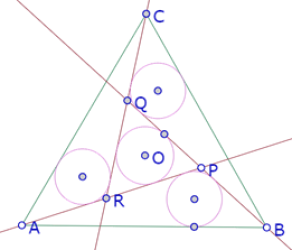
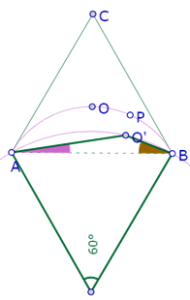
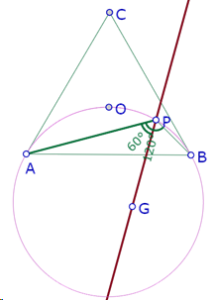
Pero también podemos hacer una construcción diferente de los círculos exteriores a PQR, de manera que tengan el mismo radio del incírculo de PQR.
Por el momento solamente vamos a construir el círculo correspondiente al triángulo APB. Ese círculo debe ser tangente a la recta PB, que también es tangente al incírculo del triángulo PQR. Si los dos círculos tienen el mismo radio, los dos centros deben estar a igual distancia de PB. Así que el centro del círculo que queremos construir está sobre una recta paralela a PB por O.
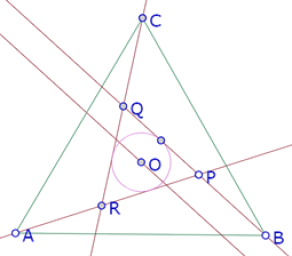
Por otra parte, si el círculo que queremos construir debe ser tangente a PB y a PA, entonces su centro debe estar sobre la bisectriz del ángulo APB.
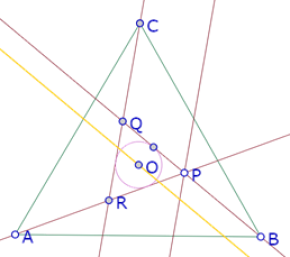
Así que ya podemos construir el círculo con centro en la intersección de esas dos rectas y con el mismo radio del incírculo de PQR.

Y constatamos que ese círculo no es tangente a la recta AB. Nuevamente, tendremos que acomodar la posición de P sobre el arco, para lograr perceptivamente esa tangencia.
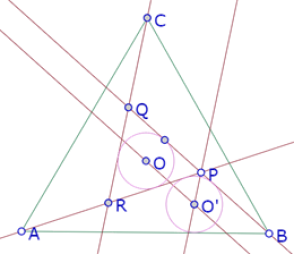
Pero esta no es una construcción exacta, puesto que al mover P no se conserva la tangencia del círculo y AB.
Hemos hecho dos construcciones aproximadas, una que garantiza que el círculo de centro O’ sea incírculo de APB, pero no garantiza que tenga el mismo radio del incírculo de PQR. Otra que garantiza que el círculo de centro O’ es tangente a AP y PB y tiene el mismo radio del incírculo de PQR, pero no garantiza que sea tangente a AB.
¿Cómo lograr garantizar todas las condiciones?
Podemos utilizar el método del lugar geométrico para resolver problemas de construcción. Ese método pide primero que todo reducir el problema de construcción a la construcción de un solo punto. En este caso, si sabemos construir el centro O’, podríamos construir ese círculo, y las rectas AP y PB tangentes al círculo. Teniendo esas rectas AP y PB podríamos hacer el resto de la construcción.
En segundo lugar, el método pide considerar dos lugares geométricos diferentes a los que pertenezca ese punto. En nuestro caso, cada una de las dos construcciones aproximadas que hemos realizado permite considerar el lugar geométrico del punto O’ con respecto al punto P. Es decir, para cada posición de P sobre el arco, hay una posición de O’.
El método nos recuerda que el punto solución está en la intersección de esos dos lugares geométricos; así que si podemos construir esos dos lugares como objetos geométricos, podremos construir su intersección y por lo tanto solucionar el problema.
Miremos experimentalmente cómo obtener esos lugares.
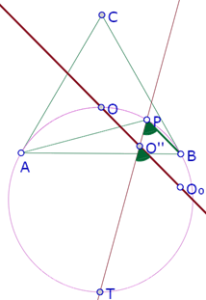
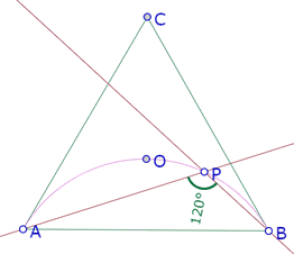
Tomemos la primera construcción, en la que O’ es intersección de las bisectrices de los ángulos APB y ABP. Activamos la traza del punto O’ y movemos el punto P. Obtenemos la siguiente imagen

La traza azul es el conjunto de las posiciones que ocupa el punto O’ en cada posición del punto P. Aparentemente es un arco de círculo de extremos A y B.
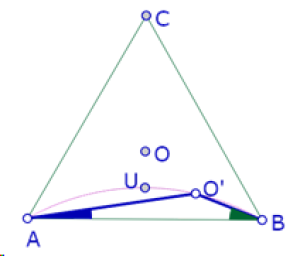
Ahora tomemos la segunda construcción, en la que O’ es intersección de la paralela a PB por O y la bisectriz del ángulo APB. Al activar la traza de O’ y arrastrar P, se obtiene la siguiente imagen
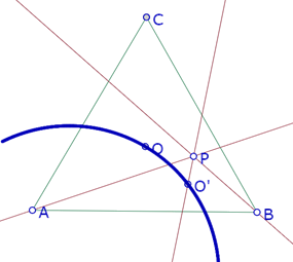
La traza parece corresponder a un arco de círculo que pasa por el punto O.
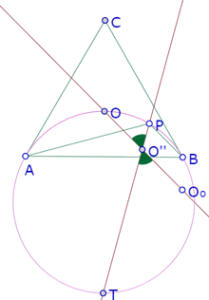
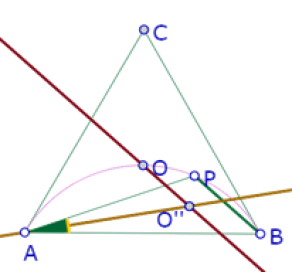
Si hacemos las dos construcciones en una misma figura y cambiamos el color de una de las trazas obtenemos la siguiente imagen
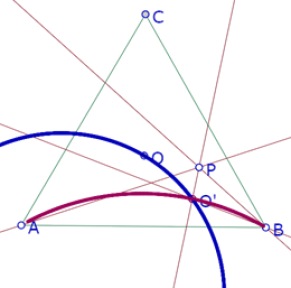
Donde podemos constatar que efectivamente los dos lugares se cortan en un punto. Ese punto es aquél en el que O’ cumple las propiedades garantizadas en la primera construcción: es equidistante de las rectas AP, PB y AB, pero también cumple las condiciones garantizadas por la segunda construcción: es equidistante de AP y PB, y su distancia a PB es la misma distancia de O a PB. Por lo tanto, si logramos construir ese punto de intersección, el círculo de centro O’ podrá ser incírculo del triángulo APB y tendrá el mismo radio del incírculo de APB.
Vamos a buscar experimentalmente una manera de caracterizar cada uno de esos dos lugares geométricos en relación con el triángulo ABC, de manera que podamos construirlos como objetos geométricos.
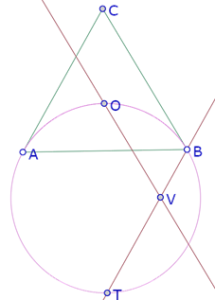
Consideremos la primera construcción (O’ es intersección de las bisectrices de APB y ABP) que produce la traza roja. Hicimos la hipótesis de que la traza es un arco de un círculo que pasa por A y B. Si podemos construir un tercer punto de esa traza, podremos construir el círculo.
Ese tercer punto puede ser el que corresponde a la posición en que P está sobre O.

Para verificar que realmente ese arco corresponde al lugar geométrico del punto O’, centro del incírculo del triángulo APB, donde P es un punto del arco AOB, es necesario comprobar que haya una correspondencia biunívoca entre los puntos del arco AOB y los puntos del arco AUB. En otras palabras, para cualquier posición de P sobre el arco AOB, las bisectrices de los ángulos APB y ABP se cortan sobre el arco AUB y para cada posición de O’ sobre el arco AUB, la recta simétrica de la recta AB con respecto a AO’ y la recta simétrica de la recta AB con respecto a BO’ se cortan sobre el arco AOB[1].
Comencemos con la primera verificación.
[1] Ya que la bisectriz de un ángulo es el eje de simetría de los lados del ángulo.
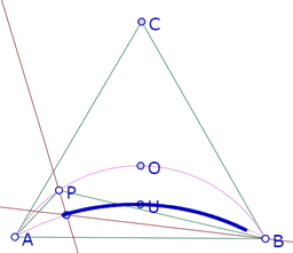
En esta imagen podemos ver que efectivamente la traza del punto de intersección de las bisectrices de los ángulos APB y ABP coincide con el arco AUB.
Ahora la segunda verificación
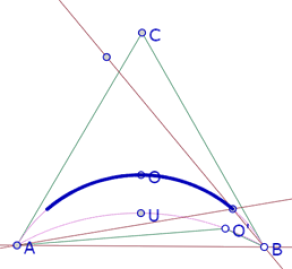
En esta imagen podemos ver que efectivamente, la traza del punto de intersección de las rectas simétricas de AB con respecto a AO’ y BO’ coincide con el arco AOB.
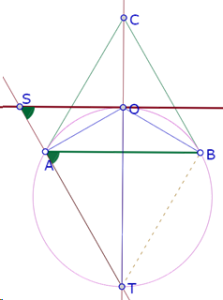
Ahora consideremos la segunda construcción (O’ es intersección de la bisectriz del ángulo APB y la paralela a PB por O). Hicimos la hipótesis de que es un arco de círculo que pasa por O.
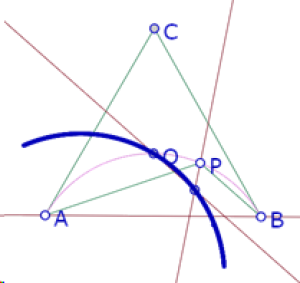
A diferencia del arco anterior, para este caso no conocemos los extremos, ya que cuando P está sobre A o sobre B, el ángulo APB queda indeterminado y su bisectriz no existe.
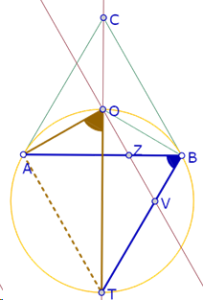
Sin embargo, al experimentar con esta construcción, podemos constatar que la bisectriz del ángulo APB parece pasar siempre por un mismo punto.
Para verificar esta hipótesis vamos a activar la traza de esa bisectriz y vamos a mover P.
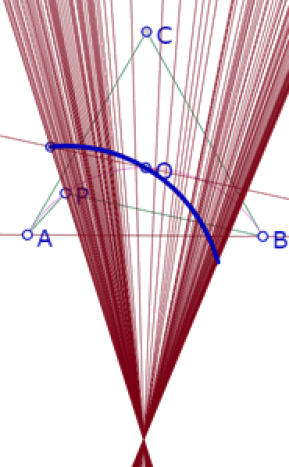
En esta imagen podemos ver que efectivamente, las bisectrices pasan todas por un mismo punto que puede construirse como intersección de dos de ellas.
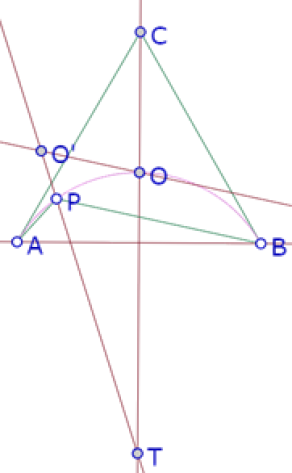
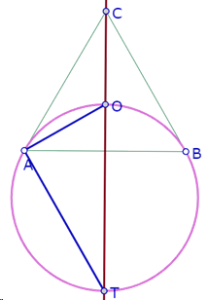
Esta propiedad nos permite construir el punto O’ para los casos extremos en que P está sobre A y sobre B, ya que las rectas TA y TB corresponderían a las bisectrices del ángulo APB en esos casos.
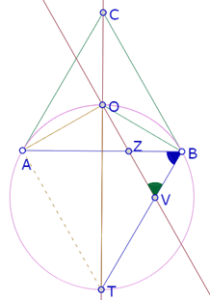
Cuando P está sobre A, AB=PB y el punto O’ es la intersección de TA y la paralela a AB por O.
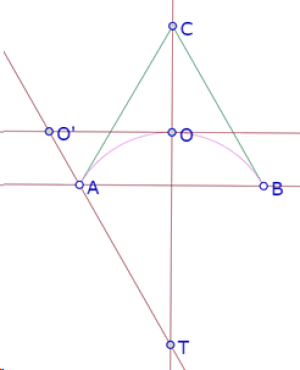
Cuando P está sobre B, la recta PB sería tangente al círculo AOB, es decir es la misma recta BC.
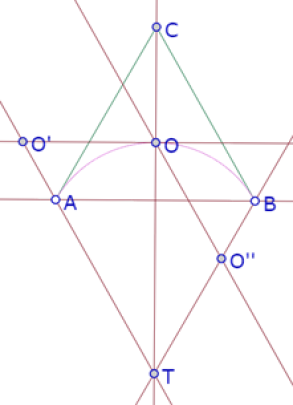
Y esos serían los puntos extremos del arco

Vamos a hacer las dos verificaciones: para todo punto P sobre el arco APB, la intersección de la paralela a PB por O y la bisectriz del ángulo APB está sobre el arco SOV. Y para todo punto O’ sobre el arco SOV, la intersección de la paralela a OO’ por B y la recta TO’ está sobre el arco AOB.
Primera verificación:
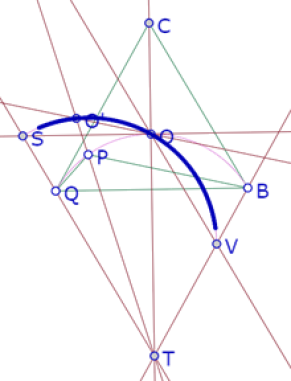
En esta imagen puede verse que la traza del punto O’ coincide con el arco SOV.
Segunda verificación:
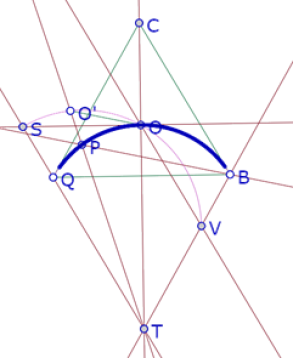
En esta imagen puede verse que la traza del punto P coincide con el arco AOB.
Así que hemos verificado experimentalmente que los arcos corresponden a los lugares geométricos del punto O’.
Podemos ahora utilizar esos dos arcos para construir la solución del problema.
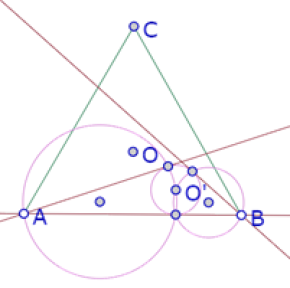
Teniendo el punto O’ podemos terminar la construcción primero construyendo el círculo de centro O’ tangente a AB.

Luego construyendo las tangentes a ese círculo que pasan por A y por B
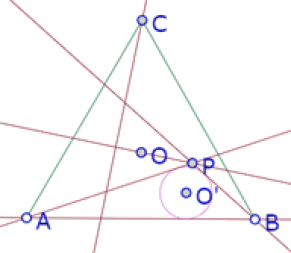
Luego construimos la recta OP y la perpendicular a OP por C.
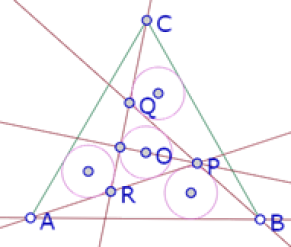
Y verificamos que los cuatro círculos tengan el mismo radio
Efectivamente, los cuatro círculos tienen el mismo radio
También verificamos que cada uno de los círculos sea incírculo del triángulo correspondiente y que todas esas propiedades se mantienen al arrastrar cualquiera de los puntos A, B o C.
Pero aquí no termina el trabajo en la solución del problema, pues esta construcción se hizo con base en hipótesis de propiedades que deben cumplirse, propiedades que encontramos de manera perceptiva en una construcción aproximada. El rigor matemático nos exige renunciar a toda hipótesis basada únicamente en la percepción. Así que necesitamos dar un fundamento deductivo a las hipótesis que formulamos a partir de la percepción.
Parte II: experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
Vamos a demostrar las hipótesis experimentales respecto a los lugares geométricos.
1. El lugar geométrico del punto O’ intersección de las bisectrices de los ángulos APB y ABP cuando P se mueve sobre el arco AOB es un arco de círculo AUB con U intersección de la bisectriz de AOB y la bisectriz de ABO
2. El lugar geométrico del punto O” interección de la bisectriz del ángulo APB y la paralela a PB por O (cuando P se mueve sobre el arco AOB) es un arco de círculo SOV, con S intersección de TA (T es el punto de concurrencia de todas las bisectrices de los ángulos APB) y la paralela a AB por O, y V intersección de TB y la paralela a BC por O.
Consideremos el primer lugar:
El ángulo APB es constante y mide 120°.
Por lo tanto, la suma de los ángulos O’AB y O’BA es 30° y el ángulo AO’B mide 150°.
Queda así demostrado que para cualquier posición de P sobre el arco AOB, O’ está sobre el arco AUB.
Ahora consideremos un punto O’ cualquiera del arco AUB.

El ángulo AO’B mide 150° porque está inscrito en el mismo arco AUB

Entonces la suma de los ángulos O’AB y O’BA es 30° porque son los otros dos ángulos del triángulo AO’B.
Como P es la intersección de la recta simétrica de AB con respecto a BO’ y la recta simétrica de AB con respecto a AO’, entonces el ángulo ABP es el doble del ángulo ABO’ y el ángulo BAP es el doble del ángulo BAO’.

Por lo tanto, la suma de los ángulos BAP y ABP es el doble de la suma de ABO’ y BAO’, es decir 60°. Y el ángulo APB debe medir 120°.
Queda demostrado que para cualquier posición de O’ sobre AUB, P está sobre el arco AOB.
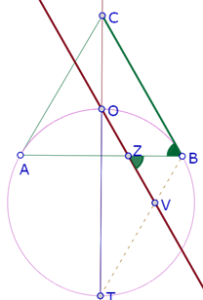
Ahora consideremos la segunda hipótesis: el lugar geométrico del punto O” interección de la bisectriz del ángulo APB y la paralela a PB por O (cuando P se mueve sobre el arco AOB) es un arco de círculo SOV, con S intersección de TA (T es el punto de concurrencia de todas las bisectrices de los ángulos APB) y la paralela a AB por O, y V intersección de TB y la paralela a BC por O.
Vamos a demostrar primero que las bisectrices de los ángulos APB cuando P se mueve sobre el arco AOB son concurrentes.
Pero esta propiedad no es suficiente para demostrar una correspondencia biunívoca entre P y O”. Necesitamos otras propiedades que se cumplan para cualquier posición de P sobre el arco AOB. Así que vamos a interrumpir nuestras deducciones para buscar experimentalmente esas otras propiedades.
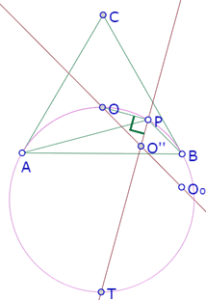
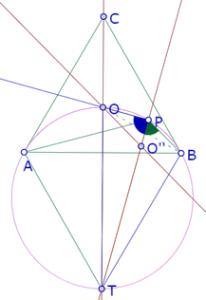
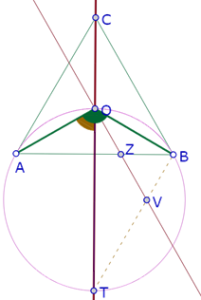
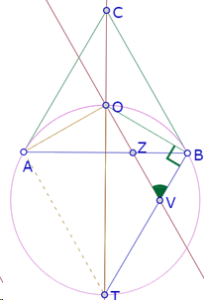
Si medimos el ángulo OPO” constatamos experimentalmente que es recto, y se mantiene recto para cualquier posición de P
Esa propiedad implica que el triángulo OPO” es un triángulo 30-60-90, y por lo tanto la longitud del segmento OO” depende de la longitud PO y la posición de OO” depende de la posición de PO, así que existe una correspondencia biunívoca entre P y O”[1].
[1] Podríamos decir que O’ es una rotohomotecia de P con respecto a O

Pero necesitamos un argumento deductivo (no experimental) para justificar que OPO’ es recto.
Así que podemos concluir que O” es el resultado de aplicar una composición de dos transformaciones al punto P: una rotación de -30° alrededor de O y una homotecia de razón
(Que es la relación entre un la altura de un triángulo equilátero y uno de sus lados).
El lugar geométrico de O” será entonces la imagen del arco AOB por esa composición de transformaciones..
Tenemos que demostrar ahora que los puntos S y V tal como los definimos en la construcción, son imágenes de los puntos A y B por esa composición de transformaciones.
El punto S es intersección de TA y la paralela a AB por O. Tenemos que demostrar que el ángulo AOS mide 30° y que
Es decir, que el triángulo SAO es un triángulo 30-60-90.
De esta manera, queda demostrado que los puntos S y V son imágenes de A y B por la composición de la rotación de -30° alrededor de O y la homotecia de razón 2/√3 con respecto a O.
Y por lo tanto, el arco SOV es imagen del arco AOB por esa misma composición de transformaciones, así que corresponde al lugar geométrico del punto O’ cuando P se mueve sobre el arco AOB.
Termina así la demostración de las dos hipótesis experimentales a la base de la solución del problema.
Coda
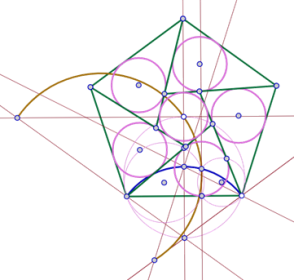
Es interesante anotar que esta solución puede generalizarse a cualquier polígono regular. Aunque no desarrollaremos esta idea aquí, nos limitamos a mostrar dos imágenes que permiten ilustrarla