Cuarto ejemplo
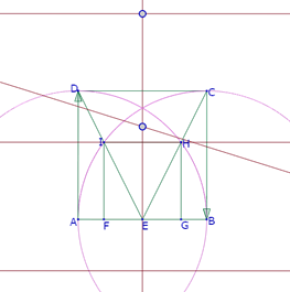
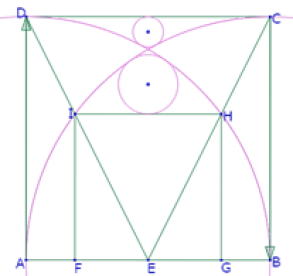
Se trata de reproducir la siguiente imagen

En la que podemos identificar las siguientes características:
Los polígonos ABCD y FGHI son cuadrados
E es punto medio de AB
a1 es un arco del círculo de centro A que pasa por B
a2 es un arco del círculo de centro B que pasa por A
El círculo c1 es tangente a HI, a1 y a2
El círculo c2 es tangente a CD, a1 y a2
Primera solución
Parte I: experimentación para encontrar una construcción exacta
Si partimos del cuadrado ABCD, podemos construir fácilmente los círculos de centro A que pasa por B y de centro B que pasa por A, y los segmentos EC y ED, que cortan esos círculos en H e I.

Los círculos c1 y c2 deben tener sus centros en la mediatriz de AB (que es eje de simetría de la figura), pero no sabemos exactamente en qué punto de esa mediatriz.
Sabemos que el centro de c1 debe estar a igual distancia de la recta IH y el círculo a2. Podemos entonces aplicar el método del lugar geométrico para encontrar la posición de ese centro.
Puesto que ese centro debe estar a igual distancia de a1 y a2, debe estar sobre su cuerda común que es la mediatriz de AB.
Por otra parte, debe estar a igual distancia de la recta IH y del círculo a2. Si podemos determinar el lugar geométrico de todos los puntos que cumplen esa condición, podremos construir ese lugar y su intersección con la mediatriz de AB, que sería la posición del centro que estamos buscando.
Así que tenemos que tratar de determinar ese lugar geométrico[1].
Hacemos una construcción con una recta y un círculo de radio fijo
[1] De todos los puntos que equidistan de una recta y un círculo.
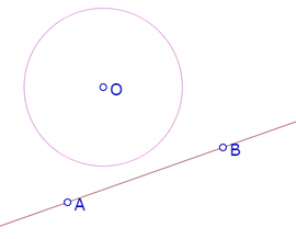
Al arrastrar cualquiera de los puntos A, B, O, podemos cambiar la relación entre el círculo y la recta, para abarcar tres casos: la recta es exterior al círculo, la recta es tangente al círculo, la recta es secante al círculo.
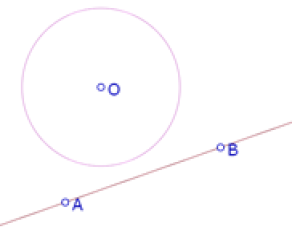
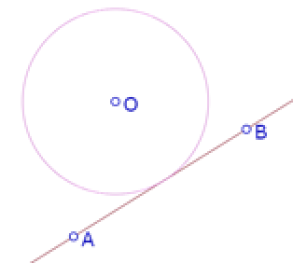
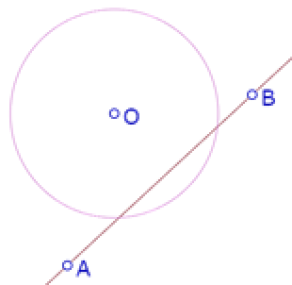
Vamos a utilizar un método llamado ‘hilvanado’ dentro de la comunidad de usuarios de software de geometría dinámica. Es un método para determinar un lugar geométrico, que consiste en acomodar muchos puntos que cumplen la condición del lugar geométrico para tratar de identificar su forma y su relación con los elementos dados en la construcción.
Debemos entonces crear puntos y acomodarlos en la construcción, de manera que estén a igual distancia de la recta y del círculo.
Pero primero debemos aclarar qué entendemos por distancia de un punto a un círculo. Como lo que estamos buscando es determinar la posición del centro de un círculo tangente a una recta y un círculo, vamos a definir la distancia de un punto a un círculo como la distancia del punto a la recta tangente al círculo por el punto de intersección del círculo y el diámetro que contiene el punto.
Dados un círculo de centro O y un punto P cualquiera, la recta OP corta el círculo en dos puntos F y G. Llamaremos distancia de P al círculo a la distancia de P a cada una de las rectas tangentes al círculo por F y por G.
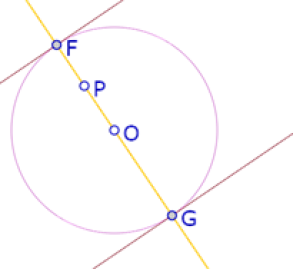
Esta definición es equivalente a decir que la distancia de un punto a un círculo es la distancia del punto a la intersección del círculo con el diámetro que contiene el punto.
Según esta definición, existen dos distancias entre un punto y un círculo.
Ahora sí podemos proceder a realizar el hilvanado correspondiente al lugar geométrico de los puntos que equidistan de un círculo y una recta.
En la siguiente imagen aparecen puntos rojos y puntos azules que corresponden a las dos distancias de un punto al círculo, en posiciones en las que el punto es (perceptivamente) equidistante del círculo y de la recta.
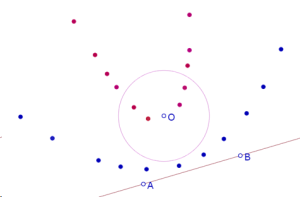
Esos dos conjuntos de puntos parecen formar dos parábolas.
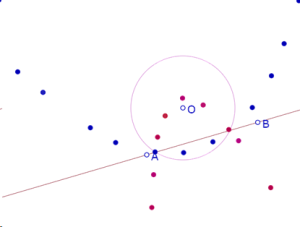
En esta configuración la recta es secante al círculo y los puntos azules y rojos siguen pareciendo formar dos parábolas.
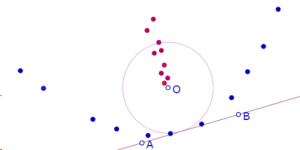
En esta configuración la recta es aparentemente tangente al círculo, y puede observarse que los puntos azules siguen formando una parábola, mientras que los rojos no representan claramente una parábola.
Sabemos que una parábola es el lugar geométrico de los puntos que equidistan de una recta y un punto. En este caso, estamos buscando el lugar geométrico de los puntos que equidistan de una recta y un círculo.
Pero si analizamos los dos casos de equidistancia que hemos señalado anteriormente
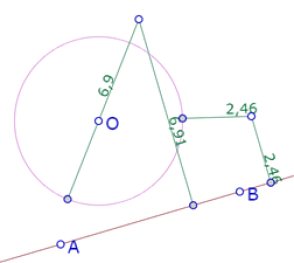
Podemos relacionar la distancia del punto al círculo con la distancia del punto al centro del círculo. En el primer caso, la distancia del punto al círculo es igual a la distancia del punto al centro del círculo menos el radio. En el segundo caso, la distancia del punto al círculo es igual a la distancia del punto al centro más el radio.
Así que el lugar geométrico de los puntos que equidistan de un círculo de centro O y una recta AB son dos parábolas de foco O, cuyas directrices son paralelas a AB y están a una distancia del radio con respecto a esa recta.

(recta AB exterior al círculo)
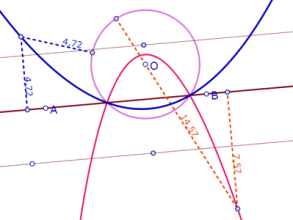
(recta AB secante al círculo)
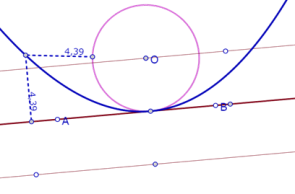
(recta AB tangente al círculo. O está sobre una de las rectas paralelas a AB, la parábola cuya directriz es esa recta no existe)
Habiendo establecido el lugar geométrico de los puntos equidistantes de un círculo y una recta, podemos utilizar el método del lugar geométrico para construir de manera exacta los centros de los círculos c1 y c2 y así dar solución al problema.
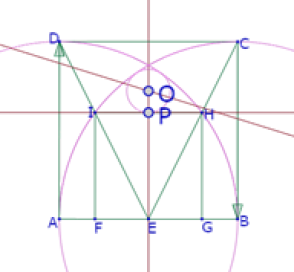
El centro de c1 debe estar sobre dos lugares geométricos: 1) el lugar de todos los puntos que equidistan de los círculos a1 y a2, que es la mediatriz de AB y 2) el lugar de todos los puntos que equidistan de HI y del círculo a1, que son dos parábolas con foco en A y cuyas rectas directrices son paralelas a HI y están a una distancia AD de esta recta.
Construimos entonces esos lugares geométricos

Vemos que hay dos puntos de intersección de los dos lugares geométricos. De los cuales nos interesa únicamente el que está entre la recta HI y la recta DC.
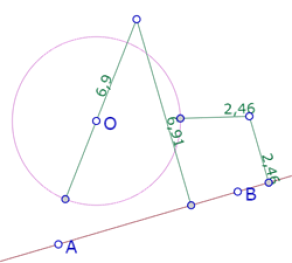
Para verificar que el círculo construido es tangente al arco a1, medimos las distancias AO, OP y AB.
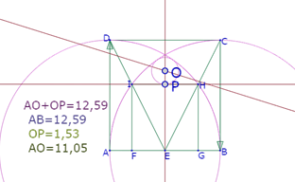
Como AO+OP=AB, los dos círculos son tangentes.
Ahora, utilizamos el mismo método para construir el centro de c2.
Sabemos que ese centro está sobre dos lugares geométricos: 1) el lugar de todos los puntos que equidistan de a1 y a2, que es la mediatriz de AB y 2) el lugar de todos los puntos que equidistan de DC y del círculo a1, que son dos parábolas de foco A y cuyas rectas directrices son paralelas a DC y están a la distancia AB con respecto a DC (como una de esas rectas es AB y contiene el foco, esa segunda parábola no existe).

Para verificar que el círculo construido es tangente a a1, medimos las distancias AO’, O’P’ y AB
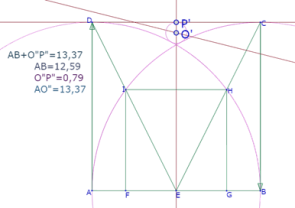
Como AB+O’P’=AO’, los círculos son tangentes.
Así que nuestra construcción es exacta
Segunda solución
Parte I: Experimentación para encontrar la construcción exacta
Volvamos a la figura inicial, sin los círculos interiores tangentes.
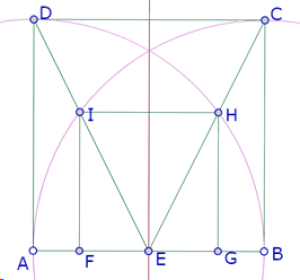
Para construir el círculo c1, vamos a garantizar su tangencia con el arco AIC creando un punto P sobre ese arco, que será el punto de tangencia.
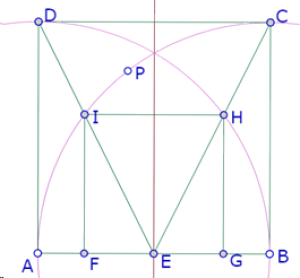
El segmento BP es el radio del círculo de centro B que pasa por A y que debe contener el centro del círculo c1. Entonces la intersección de la recta BP con la mediatriz de AB será ese centro.
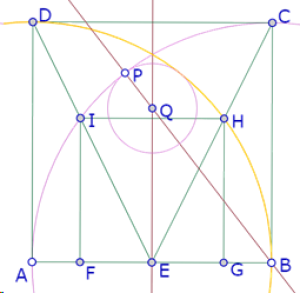
Para lograr que el círculo de centro Q que pasa por P sea tangente al segmento IH, hay que ajustar la posición de P.
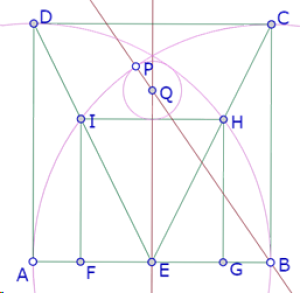
Ahora debemos encontrar la posición de P que garantiza que ese círculo sea tangente a IH.
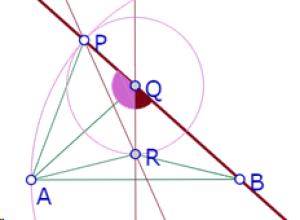
Para visualizar más claramente esa posición, vamos a construir el punto R, de intersección de la mediatriz de AB y c1, que cuando esté sobre IH será el punto de tangencia.
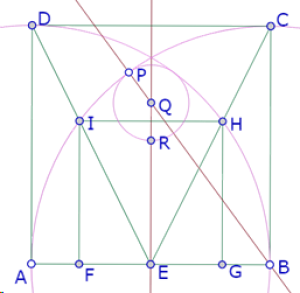
Se forma entonces un triángulo PQR isósceles en Q.
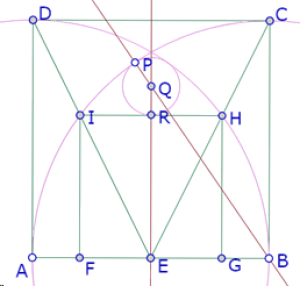
Al trazar la recta PR y mover el punto P, puede observarse que esa recta siempre pasa por un punto del círculo de centro B que pasa por A.
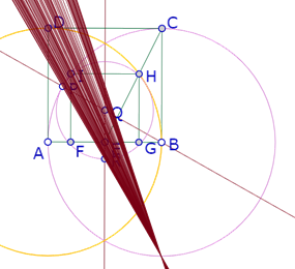
Ese punto parece ser la intersección de ese círculo con la recta BC.
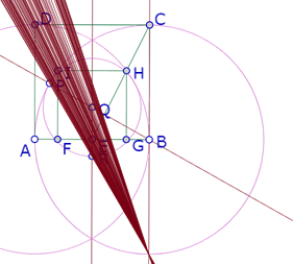
Es decir, para cualquier posición de P sobre el círculo de centro B que pasa por A, la recta PR pasa por la intersección de la recta BC y el círculo de centro B que pasa por A. Llamemos S a ese punto de intersección.
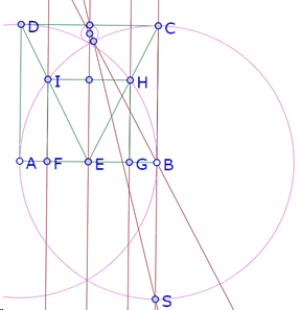
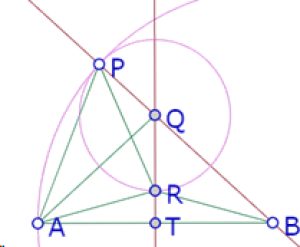
La solución se encuentra cuando el punto R está sobre el segmento HI, para lo cual basta con construir la recta que pasa por S y por el punto de intersección de HI y la mediatriz de AB.

Del mismo modo, para construir el círculo c1 se traza la recta que pasa por S y por la intersección de DC y la mediatriz de AB
Parte II: Experimentación para encontrar justificaciones deductivas para las hipótesis experimentales
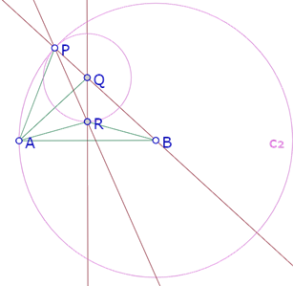
Vamos a demostrar la conjetura que permite resolver el problema: para cualquier posición de P sobre el círculo de centro B que pasa por A, la recta PR pasa por el punto de intersección de BC con el círculo.
Tenemos entonces el círculo de centro B que pasa por A, la mediatriz de AB, un punto P sobre el círculo, la recta PB, Q punto de intersección de la recta PB y la mediatriz de AB, el círculo de centro Q que pasa por P y R punto de intersección de ese círculo y la recta PB. Tenemos que demostrar que la recta PR (variable) siempre pasa por el mismo punto del círculo de centro B que pasa por A.
Una manera de demostrar que esa recta pasa por un punto fijo del círculo de centro B que pasa por A es demostrando que el ángulo APR es constante. Si ese ángulo es constante, como su vértice está sobre el círculo, sus lados tienen que pasar por dos puntos fijos de ese círculo.
Entonces intentemos demostrar que el ángulo APR es constante. Podemos relacionar ese ángulo con otros ángulos de la figura; por ejemplo, <APR=<APB-<RPB.
¿Qué podemos afirmar de los ángulos en esa figura?
Sabemos que el triángulo PQR es isósceles porque P y R están sobre el mismo círculo de centro Q. Por lo tanto, los ángulos RPQ y PRQ son iguales. Además, el ángulo RPQ es el mismo ángulo RPB.
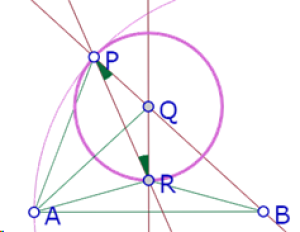
Igualmente, el triángulo ABP es isósceles porque A y P están sobre el mismo círculo de centro B. Por lo tanto, los ángulos BAP y BPA son iguales.

Por otra parte, el triángulo ARB es isósceles porque R está sobre la mediatriz de AB. Por lo tanto, los ángulos RBA y RAB son iguales.

Además, los ángulos PQR y RQB forman un par lineal, por lo tanto son suplementarios.
Ahora intentemos usar esas propiedades para calcular el ángulo APR.
Como el triángulo PQR es isósceles en Q, <PQR=180-2<RPQ.
Como los ángulos PQR y RQB son suplementarios, <RQB=180-<PQR=180-(180-2<RPQ)=2<RPQ.
Sea T el punto de intersección de AB y la mediatriz de AB.
El triángulo QTB es rectángulo, por lo tanto <QBA=<QBT=90-<RQB=90-2<RPQ.
Como el triángulo ABP es isósceles en B,
<BPA=(180-<PBA)/2=(180-<QBA)/2=(180-(90-2<RPQ))/2=(90+2<RPQ)/2=45+<RPQ.
Pero <RPA=<BPA-<BPR=45+<RPQ-<BPR=45+<BPR-<BPR=45.
De manera que el ángulo APR es constante. Por lo tanto la recta PR (variable) pasa siempre por un punto fijo del círculo de centro B que pasa por A. Pero el ángulo APR mide 45°, y el ángulo ACB mide 45°.
Como esos dos ángulos están inscritos en el mismo círculo, la recta PR y la recta CB se cortan en el mismo punto del círculo.
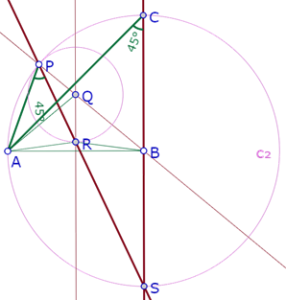
Así queda demostrado que la recta (variable) PR siempre pasa por el mismo punto del círculo de centro B que pasa por A.