Presentación del libro
Para la enseñanza de la programación según los programas (franceses de matemáticas) de 2016 para la media, los profesores tienen a disposición muchas herramientas posibles, ricas e interesantes. En Francia los profesores de matemáticas deben enseñar a programar, y esta nueva misión requiere una reflexión atenta.
Por ejemplo, es sorprendente que algunos alumnos se plantean la pregunta difícil del número 1 como neutro de la multiplicación, y esto aparece también en su práctica de programación, como invariante también en un nuevo contexto. El aprendizaje de la programación puede entonces aportar otro punto de vista, más operativo, sobre las matemáticas. Como introducción a lo que presentaremos en este libro, aquí hay dos programas de alumnos de octavo grado, sobre la producción de figuras construidas alrededor del ciclo 1-2-3 (espiroláteros, ilustrados en diferentes partes del libro). Una concepción aditiva de la secuencia 1-2-3 produce soluciones simples.
Una concepción multiplicativa de esta misma secuencia plantea dificultades.
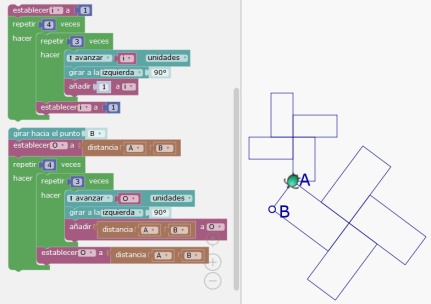
En el caso de una estrategia multiplicativa, el alumno tiende a suprimir un bucle y construir uno por uno los trazos de la tortuga. Para evitar eso, hay que multiplicar por 1, algo que no es natural para muchos alumnos.
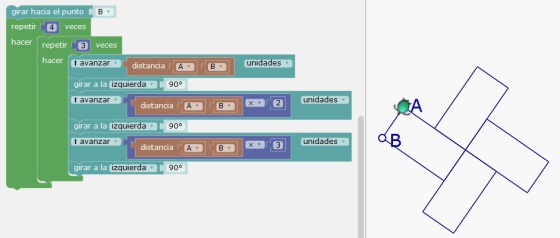
En esta situación, la presentación del bloque contador, con su variable que puede tomar valor 1 en una multiplicación, es una manera eficaz que permite encontrar, con dos bucles imbricados, una estructura cercana a la estrategia aditiva. También permite al profesor explicitar la relacio´n con la representación de la unidad en preguntas algebraicas como factorizar 3n+n donde el segundo 3 debe verse como 3x1.
La práctica de una programación lúdica, en este caso para producir una figura dinámica, con posibilidad de manipulación directa, es una oportunidad de hacer vivir las matemáticas de manera diferente, ya sea aritmética elemental, o geometría utilizando la tortuga, para hacer aparecer las propiedades de los cuadriláteros.
de manera más sorprendente, ya que está en un entorno dinámico, la tortuga da la oportunidad de algebrizar algunos de los problemas, y por lo tanto, resolverlos sin ningún cálculo, simplemente porque se plantean de manera algebraica. Esta estrategia estará presente en todo el libro, aunque se dedicará un capítulo especialmente. Es importante porque muestra el álgebra por lo que es realmente: una manera de estudiar un problema, una conceptualización diferente (de la aritmética) de la modelación de situaciones.
Este libro trata de la práctica de Blockly, implementado en un entorno dinámico de geometría. Este encuentro entre una programación visual dinámica y un soporte de objetos que pueden manipularse abre perspectivas de una gran originalidad en varios campos - como la algebrización de la tortuga.
También se abordarán otros dos campos innovadores. En efecto, la tortuga dinámica en un entorno 3D renueva completamente la relación con la enseñanza de la 3D, con actividades lúdicas, creativas, simples y ricas en reflexiones geométricas. Se dedicará un capitulo a este tema, y por el placer del autor, una galería 3D.
Finalmente, gracias a una implementación particular como comportamiento de los objetos, Blockly permite una rutpura controlada del determinismo de la geometría dinámica. Lo cual permite realizar actividades que no son posibles de otra manera (ver últimos capítulos). El software CaRMetal ya permitía esa ruptura controlada del determinismo. Pero aquí, además, lo táctil añade una dimensión kinestésica que produce sentido en clase tanto en el campo geométrico como en el campo funcional.
En un capítulo preliminar se presenta la interfaz de DGPad. En efecto, un mínimo de apropiación de las ideas básicas de su interfaz (herramientas infijas en lugar de prefijas) permite ser más eficaz luego en la programación.
Deseo que tengan un descubrimiento y exploración agradables de este encuentro con la programación por bloques y la geometría dinámica en el software DGPad.