Blockly y tortuga dinámica con DGPad

Este resultado puede sorprender. El círculo está realmente en un plano, ¿o es una aproximación? ¿Si es un plano cuál es su dirección? Gracias a Dominique Tournes, director de nuestro IREM, tenemos una respuesta. Nos ubicamos en el sistema inicial de coordenadas de la tortuga, en A, con sus direcciones \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) .

La tortuga avanza primero d en la dirección \(\overrightarrow{i}\), que corresponde a una traslación de vector \(d\overrightarrow{i}\). Luego hace sucesivamente tres rotaciones "estáticas" o sea tres rotaciones vectoriales. La primera, de ángulo -h, alrededor de \(\overrightarrow{j}\), transforma el sistema \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) en \((\overrightarrow{i}_{1},\overrightarrow{j}_{1},\overrightarrow{k}_{1})\) por la matriz \(M_{1}=\begin{pmatrix}\cos h & 0 & -\sin h\\ 0& 1 &0 \\\sin h &0 &\cos h\end{pmatrix}\). La segunda, de ángulo g, alrededor de \(\overrightarrow{k}_{1}\), transforma \((\overrightarrow{i}_{1},\overrightarrow{j}_{1},\overrightarrow{k}_{1})\) en \((\overrightarrow{i}_{2},\overrightarrow{j}_{2},\overrightarrow{k}_{2})\) por la matriz \(M_{2}=\begin{pmatrix}\cos g & -\sin g &0\\\sin g& \cos g &0 \\0 &0 &1\end{pmatrix}\). Finalmente, la tercera, de ángulo -h alrededor de \(\overrightarrow{j}_{2}\) transforma \((\overrightarrow{i}_{2},\overrightarrow{j}_{2},\overrightarrow{k}_{2})\) en \((\overrightarrow{i}_{3},\overrightarrow{j}_{3},\overrightarrow{k}_{3})\) por la matriz inicial \(M_{1}\). La composición de las tres, el palíndromo \(M_{1}M_{2}M_{1}\), tiene matriz \(M=\begin{pmatrix}\cos^{2}h.(1+\cos g)-1 & -\sin g\cos h & -\sin h\cos h.(1+\cos g)\\ \cos h\sin g& \cos g &-\sin h \sin g \\\sin h\cos h.(1+\cos g) &-\sin g \sin h &1-\sin^{2}h.(1+\cos g)\end{pmatrix}\), expresión de \((\overrightarrow{i}_{3},\overrightarrow{j}_{3},\overrightarrow{k}_{3})\) reportado a \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\).

Es una isometría vectorial positiva, de dirección propia la recta vectorial \(\left\{\begin{matrix}X=0\\ (\cos g-1)Y-\sin h\sin gZ=0\end{matrix}\right.\)

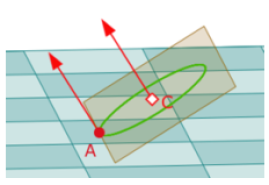
Entonces es una rotación vectorial alrededor del eje (0, sinhsing,cosg-1). El plano vectorial P ortogonal al eje contiene \(\overrightarrow{i}\) y es estable por la transformación. La tortuga avanza entonces en el plano de dirección P que pasa por A.

Luego de un movimiento elemental, su orientación está dada por el vector \(\overrightarrow{i}_{3}\), que pertenece a P como imagen de \(\overrightarrow{i}\). Se encuentra entonces en la situación inicial y por lo tanto, por iteración, la tortuga no sale del plano de dirección P que pasa por A.

El extremo del vector normal al plano en A, está dado por la siguiente expresión, donde el coeficiente 100 es arbitrario [X,Y]=A-100*[0,sin(alto)*sin(izquierda),cos(izquierda)-1].

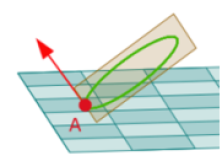
Centrar el vector normal

La trayectoria de la tortuga no es un círculo, sino una línea poligonal. El valor del parámetro d, pequeño con respecto a la resolución de las pantallas, puede dar la ilusión de círculo. Patrice Dbrabant nos dió una respuesta a este problema. Se trata de calcular un valor aproximado del radio de esa línea poligonal.

La componente \(\overrightarrow{i} \) del vector \(\overrightarrow{i}_{3}\) puede escribirse también \((\cos^{2}h)(1+\cos g)-1=\cos^{2}h\cos g- \sin^{2}h\). Entonces el ángulo de la línea poligonal es \(\alpha =\cos ^{-1}(\cos ^{2}h\cos g-\sin ^{2}h)\). Por lo tanto, el radio del círculo aproximado es \(R=\frac{360}{\alpha }*\frac{d}{2\pi }=\frac{180d}{\alpha \pi }\) si el ángulo está en grados.

No obstante hay que adaptar la unidad porque d está en pixeles: nótese el bloque que permite utilizar la unidad en pixeles (Pu es el vector unitario en la dirección conveniente)

En un hermoso artículo de agosto de 2017 sobre los espiroláteros, Patrice precisa que como se aplica un palíndromo de tipo T=BAB con la tortuga 3D, la iteración de la transformación es coplanar. Como \(T^{-1}=B^{-1}A^{-1}B^{-1}\) utiliza la misma serie de rotaciones (mismo orden), con ángulos opuestos, el resultado es coplanar, mientras que con T=AB y \(T^{-1}=B^{-1}A^{-1}\) no sucede lo mismo.