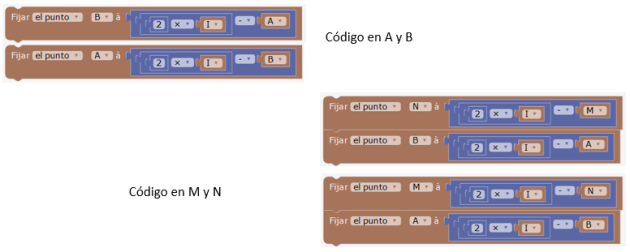
Referencia cruzada de puntos
El comportamiento flexible de Blockly sobre los puntos permite ir más lejos no solo técnicamente, sino también didácticamente, para proponer modelaciones más cerca de las definiciones. Es el caso de los puntos simétricos: dos puntos son simétricos con respecto a un punto I si I es su punto medio. Modelar esta definición en geometría dinámica equivale a construir una figura en la que un punto no quede independiente y el otro dependiente, sino que si A y B son simétricos con respecto a I debería poder arrastrarse los tres puntos A, I , B. Es lo que vamos a lograr con Blockly, de manera muy simple: solo hay que escribirlo. Es la implementación de Blockly la que logra que todo funcione. Consideramos dos círculos de radio fijo, de centro M y N simétricos con respecto a I. Se coloca A y B sobre cada uno de los círculos, también simétricos con respecto a I. Todos esos puntos pueden arrastrarse.
¿Cómo es posible?¿Por qué A y B siguen estando sobre los círculos aun cuando los arrastramos?
La respuesta es simple: hay una mezcla de tipos. A y B están imantados a 5000 pixeles (muy fuertemente) a los círculos; por eso no se salen de ellos. Lo vemos en el siguiente código de la figura, mg es el nombre interno del magnetismo.

Figura dinámica 12.3 - Uso didáctico de la referencia cruzada - Puntos simétricos
Extensión de virtualización de definiciones. En la siguiente figura extendemos el principio de referencia cruzada a la referencia cruzada múltiple. Construimos un cuadrado ABCD de centro O, donde se puede arrastrar A, B, C o D, incluso O. El cuadrado es de centro O que pasa por A pero también de centro O que pasa por B. Es otro tipo de cuadrado...
Figura dinámica 12.4 - Referencias cruzadas múltiples - Ejemplo de un cuadrado