Blockly y tortuga dinámica con DGPad

Vamos a ver en algunos ejemplo lo que entendemos por reacción en tiempo real de la tortuga. En la siguiente ilustración, si se coloca en el bucle el bloque Avanzar, la tortuga avanza inmediatamente.

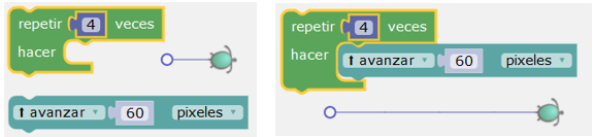
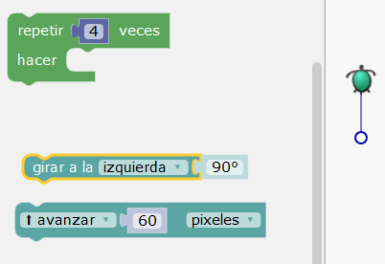
En la siguiente ilustración, puede verse el punto a la derecha de la ventana de Blockly (aunque esta ventana es transparente). Los bloques se sueltan en el espacio de trabajo arrastrándolos, o simplemente tocándolos. Al arrastrar el bloque girar, incluso antes de soltarlo, la trayectoria de la tortuga se modifica.

Riqueza de la reactividad de la tortuga: después de hacer un cuadrado usual, se puede seleccionar el ángulo. Aparece un transportador en el que puede seleccionarse el ángulo (con un paso de 15°). Puede verse el potencial de exploración "en acto".

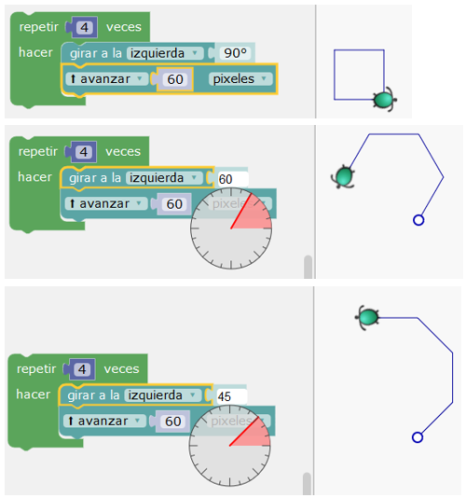
Por supuesto, al hacerlo, los alumnos pueden luego modificar el número de segmentos en el bucle repetir para terminar los polígonos regulares. Rápidamente se plantea la pregunta por la relación entre el número de lados y el ángulo de giro de la tortuga.

Primera actividad propuesta en la página siguiente: paso de lo numérico a lo algebraico.

En esta actividad comenzamos construyendo 6 hexágonos con giro de 60°.

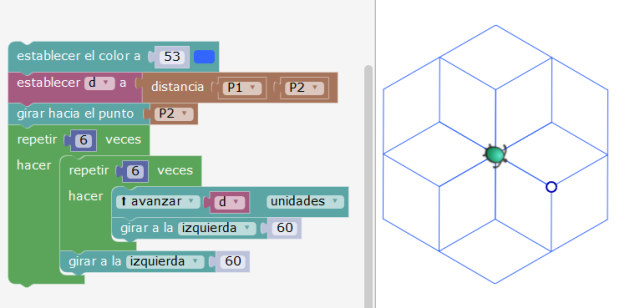
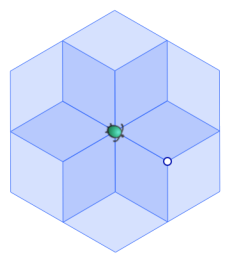
Para ver bien lo que sucede y cuestionar a los alumnos, añadimos un llenado a 20% de cada hexágono, y preguntamos a los alumnos: ¿por qué hay partes más oscuras?

Modificación 1: en la página siguiente, la figura ya está hecha, y contiene un cursor n. La idea es remplazar el hexágono por un polígono de n lados. Tiene que activar el Blockly, el código está en el punto del centro. Luego seleccionar en Expresiones el bloque de objetos, y seleccionar n en la lista desplegable (que muestra inicialmente P1).

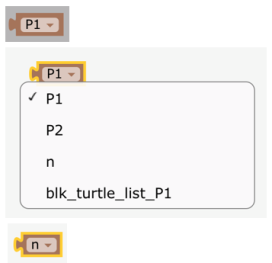
Luego duplicar dos veces este bloque (toque prolongado) porque se necesitan dos para los límites de los bucles y uno para la rotación de la tortuga, expresión que también hay que duplicar porque se usa dos veces.

Para n=8, por ejemplo, puede preguntarse de nuevo a los alumnos porqué aparecen tres niveles de colores.

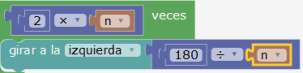
Modificación 2: luego se puede doblar el número de iteración del bucle exterior y dividir por dos el ángulo de rotación que pasa de un polígono al otro. Más adelante propondremos otra modificación.