Blockly y tortuga dinámica con DGPad

Podría pensarse que la tortuga sólo es euclidiana, ya que se avanza siempre una longitud dada: así que no tiene nada de afin. sin embargo vimos en los ejemplos anteriores - sobre el paralelogramo o la traza del ortocentro - que ciertos avances de la tortuga puende considerarse como afines cuando traducen relaciones baricéntricas. Por ejemplo, tomar la longitud inicial entre dos puntos puede considerarse como una definición de un sistema afín sobre una recta. Igualmente, el bloque que permite girar la tortuga hacia un punto no se considera euclidiano, se trata de la utilización de una regla, para unir dos puntos: la recta es una herramienta afín.

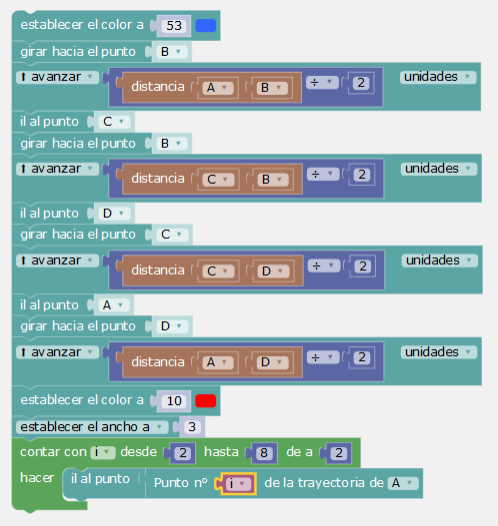
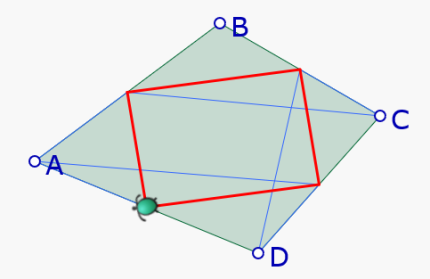
En esta construcción los vértices del paralelogramo son un punto de cada dos de la trayectoria de la tortuga. Por eso la construcción final con un contador que recorre los puntos de indice par.

Utilización del teorema de Varignon - Versión euclidiana

En la construcción anterior, no se podía dar una dirección particular a la tortuga para recorrer las rectas de los puntos medios de los diferentes triángulos. Para hacerlo, hay que utilizar un ángulo: es la frontera entre una estrategia afín y una estrategia euclidiana. La trayectoria es mucho más corta, aunque el código no es significativamente más corto.

En esta construcción, los ángulos nos permiten construir las paralelas a las diagonales AC y BD, lo que necesita girar hacia los vértices del cuadrilátero.

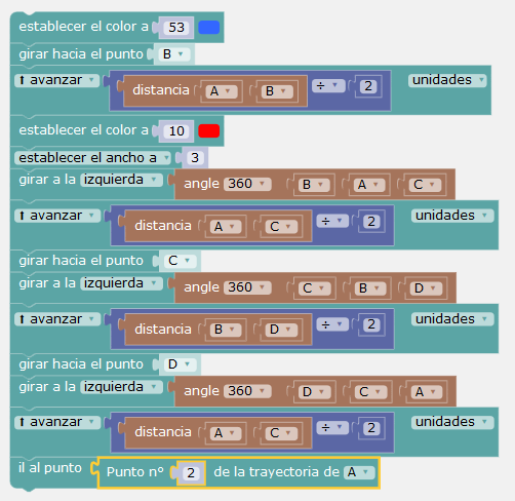
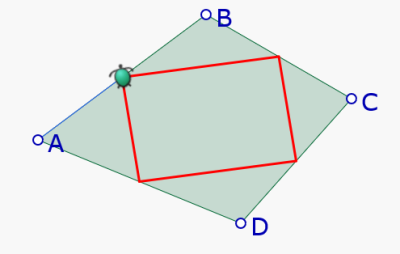
Aunque la distinción entre afín y euclidiano no hace parte de los programas escolares, esta pregunta puede ser interesante de plantear en la formación de profesores.