Blockly y tortuga dinámica con DGPad

Las relaciones de Euler en el triángulo son ocasión de revisitar un camino hacia el ortocentro para la tortuga y el trazado de la recta de Euler. Para hacerlo hay que colocar el centro del circuncírculo, con la tortuga.

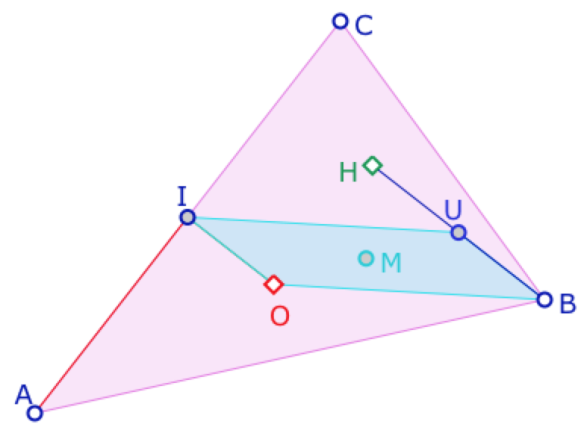
I es punto medio de A y C, O es el centro del circuncírculo. Si U es punto medio de BH, además de estar sobre el círculo de Euler, sabemos que \(overrightarrow{BH}=2\overrightarrow{OI}\) y que BUIO es un paralelogramo de centro M punto medio de IB. Si se sabe construir el centro O, se tiene entonces una traza de la tortuga que puede ir de un vértice al ortocentro - usando paralelogramo por "posición de la tortuga" - puede ser el trayecto AIMUH.

Vamos a utilizar el punto O para apuntar hacia el, así que debe existir en la figura. Se construye antes, como el punto G en un ejemplo anterior,

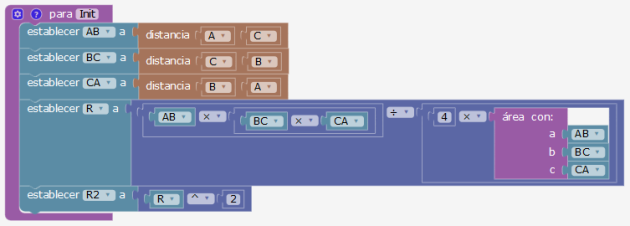
Circuncentro (del circuncírculo de radio R, para un triángulo de lados a, b y c)

Suponemos conocer la fórmula de Heron \(S=\sqrt{p(p-a)(p-b)(p-c)}\) con \(p=\frac{a+b+c}{2}\) y la relación \(r=\frac{ABC}{4S}\)

Comenzamos por un procedimiento Area y otro Init que fija las variables (globales) y el radio R.

Luego otro procedimiento coloca O haciendo un test para saber si está en el interior o en el exterior del triángulo.

Colocar el centro O del circuncírculo

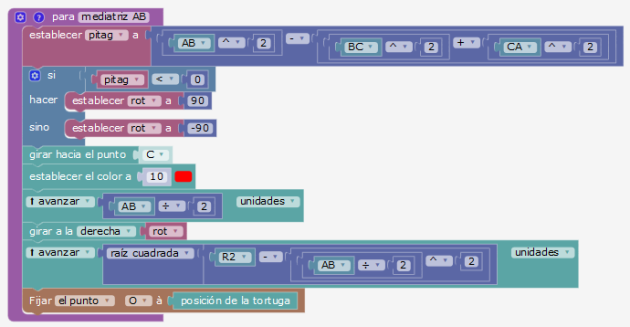
Aquí vemos nuevamente el cambio de marco de la tortuga y del código, invitando a buscar criterios métricos para saber si la tortuga, al llegar al punto medio de un segmento, debe girar hacia el interior o hacia el exterior del tríangulo para colocar O. Sabemos que el punto O es´ta en el punto medio de AB SSI \(AB^{2}-BC^{2}-CA^{2}\) es nulo (porque AB es la hipotenusa). Como O está sobre la mediatriz de AB, el signo de la expresión Pitag el que precisa la posición de O. Si es negativa, el centro del círculo está en el interior del triángulo, si no está en el exterior. Es el objeto del siguiente procedimiento para colocar O.

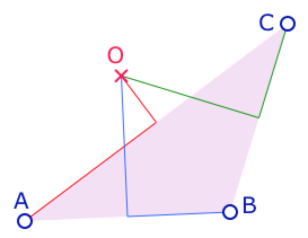
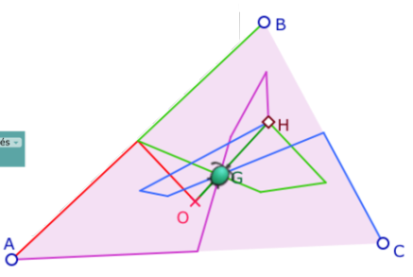
Podemos ahora hacer una traza de tortuga para ir de un vértice al ortocentro de un triángulo, y proseguir sobre la recta de Euler.

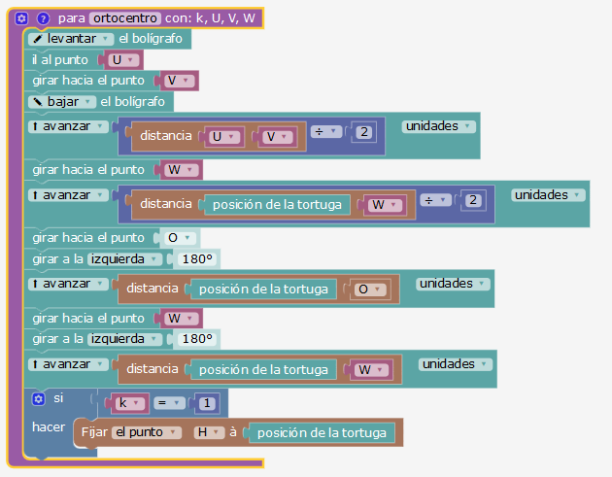
El parámetro k: se aplica el procedimiento 3 veces, pero el punto H solo hay que ubicarlo una vez. Se hace si k=1.

La traza ortocéntrica: se retoma lo que dijimos sobre la relación de Euler. Detallamos el trayecto saliendo de A con los parámetros A, B y C. Se comienza avanzando la mitad de AC, luego de la mitad de la posición de la tortuga al tercer vértice B (pasando por G). Luego, se gira hacia el centro del circuncírculo y se retrocede la distancia que separa la tortuga de ese punto. Se reitera luego con el vértice para llegar al ortocentro. Así que esta traza utiliza 3 veces la posición de la tortuga de manera algebraica.

La recta de Euler: se trata de colocar luego G y construir OH por ejemplo así:

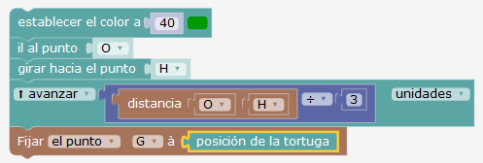
La página siguiente propone estas construcciones, y tiene disponibles los procedimientos descritos.