Las expresiones
Ya hemos visto usos bastante sofisticados de las expresiones como programas JavaScript, pero las expresiones intervienen en situaciones más elementales, como la utilización de variables.
El nombre de un objeto como variable algebraica
Como todos los software contemporáneos de geometría dinámica, el nombre de un objeto es una variable que puede usarse en una expresión o un programa. Por ejemplo, el nombre de un segmento designa su longitud, el de un círculo su radio, el de un polígono su área, algebraica, dependiendo de la orientación del polígono.
En la siguiente figura, I es el centro del círculo inscrito, y w el centro del círculo que pasa por los puntos medios de los lados del triángulo inicial. Queremos ilustrar (o conjeturar según el contexto) que esos dos círculos son tangentes.
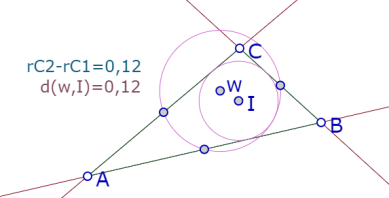
Nota práctica: si quiere finalizar esta construcción a partir de la figura del numeral anterior, basta con utilizar la herramienta "círculo por tres puntos" para construir el círculo de Euler. El centro se crea pero queda oculto. Hay que mostrarlo y darle un nombre.
Luego se crean dos expresiones, una es la diferencia de los dos radios de los círculos (sus nombres) y la otra la distancia entre los dos centros.

Que esas expresiones verifican efectivamente que los círculos son tangentes es un trabajo - en general no trivial - sobre la desigualdad triangular.
El módulo expresión como graficador
Así como cuando una expresión tiene límites se interpreta como un cursor, cuando contiene una variable estándar como x, y o t, se considera como una relación funcional. El módulo expresión se convierte en un graficador y propone trazar la representación gráfica, con un nuevo ícono de tipo parábola.
Esta característica puede convertirse en una herramienta didáctica, ya que ese ícono solo aparece si la escritura tiene una sintaxis correcta como la siguiente.
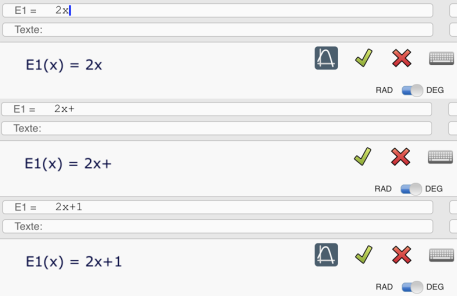
Nótese la escritura funcional de la expresión E1, con E1(x). Al tocar el icono aparece la gráfica, la expresión desaparece pero no se ha perdido, está incorporada en el gráfico que se convierte en un objeto geométrico. Pueden definirse límites de la gráfica.
A propósito del teclado de DGPad: en el computador, es posible escribir todo menos la potencia: el símbolo ^ debe escribirse desde el teclado DGPad.
Por supuesto, es posible incorporar todas las otras variables numéricas de la figura en una expresión funcionar, como los cursores.
Sin entrar en detalle, señalamos que varias herramientas estan disponibles, como d (encima de \( \Pi\) ) que corresponde a la derivación.
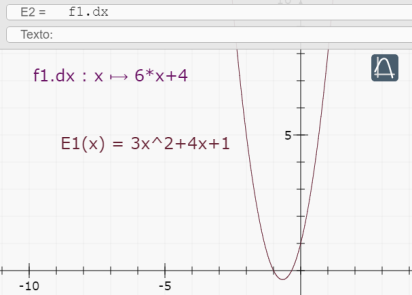
Y al validar, con el icono de la gráfica, la expresión E2 queda como se ve a continuación.
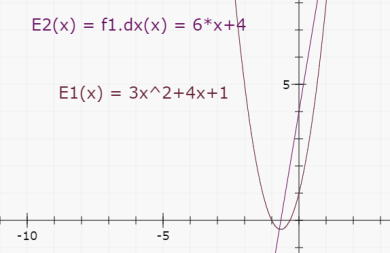
La decisión de escribir dx se debe a que pueden trabajarse varias variables, pero no seguiremos desarrollando esta idea aquí.
En geometría dinámica se pone el acento en la manipulación directa. A continuación dos figuras sobre ese tema. Primero, las tangentes comunes a dos parábolas definidas cada una por 3 puntos. Luego, ¿bajo que condiciones esas dos tangentes pueden coincidir?