Blockly y tortuga dinámica con DGPad

El rombicuboctaedro como 6 octaedros regulares

Desde el punto de vista estándar de los poliedros semi-regulares, está compuesto por 8 triángulos (uno en cada vértice de un cubo que se imagina truncado) y 18 cuadrados: 6 que corresponden a las caras de un cubo inicial y 3 veces cuatro cuadrados (en la siguiente figura arriba, en el medio y abajo) para unir los cuadrados entre ellos. También tiene 48 aristas.

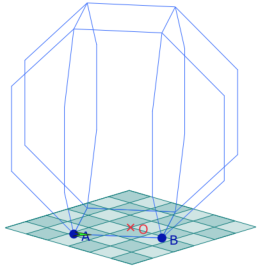
Realizar una figura -mas o menos optimizada - con la tortuga es la oportunidad de desconstruir esta representación y construir otra. En la figura precedente pueden verse 4 octógonos regulares verticales, cada uno por una arista del cuadrado de base de lado AB, y 2 octógonos regulares horizontales. Como los octógonos pueden producirse con girar 45°, estas construcciones pueden hacerse en la media. Proponiendo un cambio de marco a la vez nuevo y operacional, se permite abordar de manera diferentes la geometría del espacio y algunos poliedros.

Asumiendo este enfoque, decidimos diferenciar la parte vertical de la parte horizontal para cortar la construcción en etapas. Probablemente podríamos conceptualizar un poco más. Haciendo 8 segmentos para el octógono, la tortuga vuelve a su posición de partida, por eso se necesita avanzar en el procedimiento de la Parte Vertical.

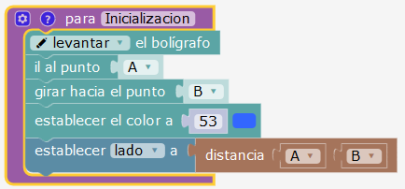
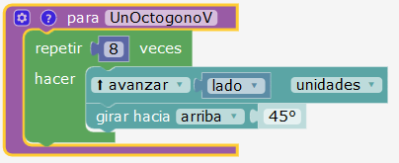
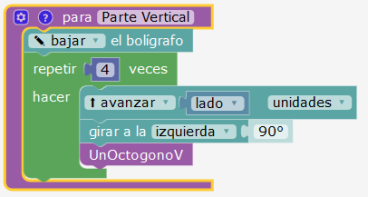
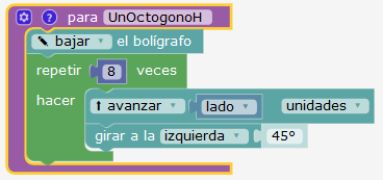
Parte vertical 1 paso

La rotación de 90° permite recorrer el cuadrado del piso y trazar los 4 octógonos. El repetir 4 veces puede interpretarse como una factorización de la tarea.

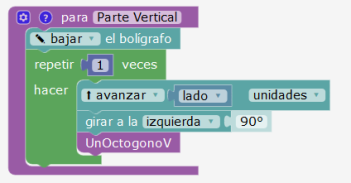
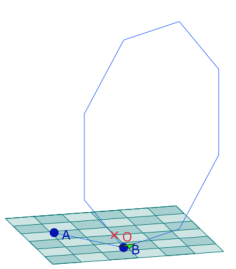
Parte horizontal

Como la tortuga llega después de la parte vertical al lugar de partida, podemos ilustrar la parte horizontal como sigue. Se trata de colocar la tortuga en el lugar adecuado, sin calcular distancias, simplemente recorriendo las aristas.

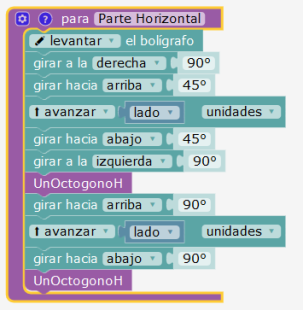
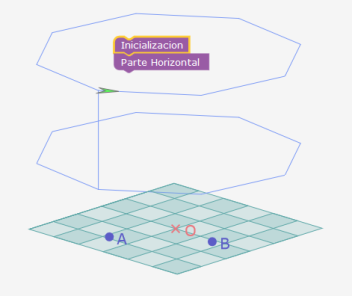
Octógono horizontal

Está en un plano orientado como el piso y por lo tanto utiliza el comando plano girar a la izquierda. Debería poder utilizarse el mismo procedimiento para los dos octógonos.