Curva de Polya
La curva de Polya es otro ejemplo de lo que puede hacerse con la tortuga dinámica, y en particular, por la estrategia dinámica, observar ejemplos de regularidad interesantes. Partimos de un triángulo ABC rectángulo en A. Se divide en dos triángulos semejantes con la altura. La primera etapa de la curva va de B a C pasando por los dos centros de gravedad de los dos triángulos. Luego se itera el procedimiento. La curva de Polya es la curva límite. Polya la estudió porque es una curva que rellena, y en el caso de un triángulo rectángulo no isosceles, tiene propiedades diferentes en particular a la de Peano.
En el caso de un triángulo rectángulo isósceles, la curva de Polya es un caso particular de la curva de Cesaro. En los demás casos, a diferencia de la curva de Cesaro que no es derivable en ningún punto, la de Polya es derivable casi en todos los puntos para un ángulo B entre π/12 y π/6, incluso con una derivada casi nula para un ángulo inferior a π/12.
Aconcejamos este artículo de Jean Pierre Kahane en Repere IREM 29 (octubre de 1997)
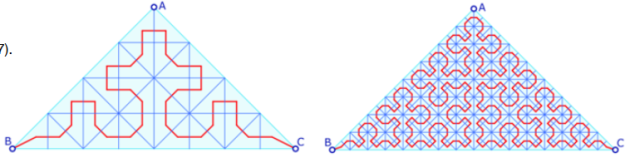
Construcción de la curva de Polya
Para ilustrar la construcción mostramos una versión final, con los triángulos. En este figura, el código está en A y la pestaña de inicialización pone la tortuga en B.
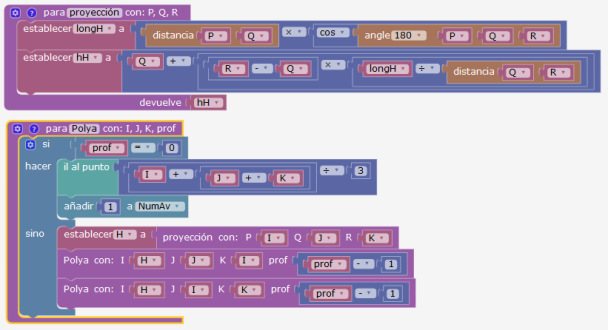
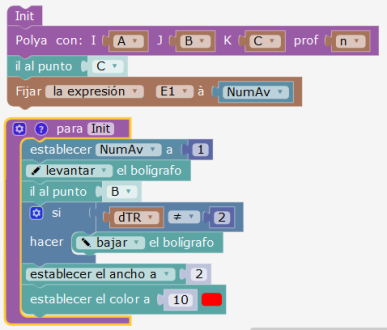
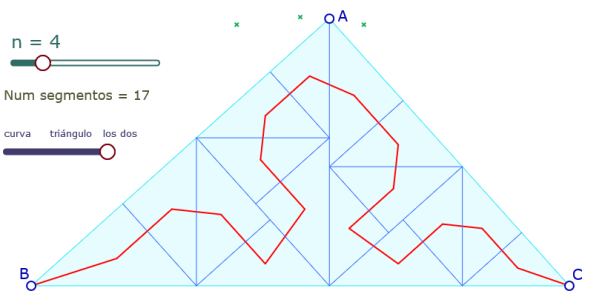
La construcción de los triángulos
La tortuga está inicialmente en A (ángulo recto). Si la profundidad es no nula, se calcula el pie de la altura. Se va a ese punto, luego se lanza la recursividad sobre la primera rama (uno de los dos triángulos), luego se vuelve a H y se lanza de nuevo la recursividad sobre la otra rama (segundo triángulo).
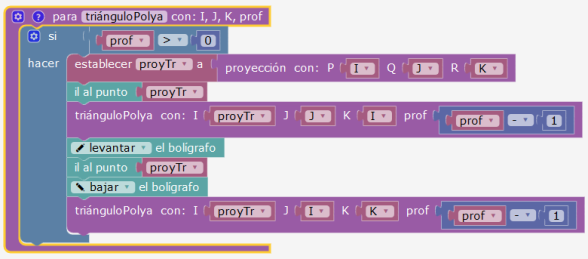
En la figura final añadimos un cursor, lo que la hace un poco más lenta.
Alineaciones particulares - El número de oro en la curva de Polya
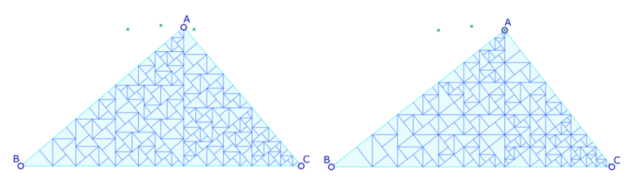
Al mover el punto A, hay casos particulares de alineaciones de los vértices de los triángulos (a la derecha A está sobre uno de los tres puntos verdes). Esas alineaciones se dan, por ejemplo, cuando el ángulo en B cumple cosθ=tanθ lo que corresponde a dos ángulos complementarios, de los cuales uno es \(sen^{-1}(\varphi -1)\) donde φ es el número de oro.